Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 46
Na figura abaixo ambas as extremidades do manômetro são abertas à atmosfera. Calcule a densidade do fluido X.
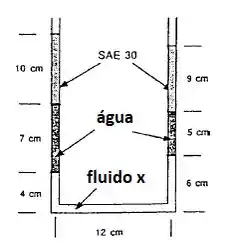
Passo 1
Bem, mais uma vez precisamos lembrar do principal conceito em hidrostática: para uma mesma altura a pressão será igual. Então olhando pra nossa figura podemos perceber que as pressões na base do tubo em U serão iguais, certo?
Passo 2
Vamos então escrever nossa equação!!!
Note que na equação acima eu já descontei a pressão atmosférica porque ela irá se cancelar, pois aparece igual nos dois lados da igualdade, show?
O subíndice “r” indica right e “l” indica left!!!
Passo 3
Agora é isolar e ser feliz!!!
Os valores das densidades são do óleo SAE e da água são: 872 kg/m³ e 979 kg/m³, respectivamente.
Substituindo os valores, vamos obter ao final:
Resposta
Exercícios de Livros Relacionados
A leitura de um medidor de pressão conectado a um tanque é de 500k P a em um local onde a pressão atmosférica é de 94k P a . Determine a pressao absoluta no tanque.
A leitura de um medidor a vácuo conectado a um tanque é de 30k P a em um local onde a leitura barométrica é de 755m m H g . Determine a pressão absoluta no tanque. Tome ρ H g= 13,590k g / m 3 .
O barômetro básico pode ser usado para medir a altura de um prédio. Se as leituras barométricas nas partes superior e inferior de um prédio são de 730m m H g e 755m m H g , respectivamente, determine
Determine a pressão exercida sobre um mergulhador a 30m abaixo da superficie livre do mar. Considere uma pressão barométrica de 101k P a e uma gravidade especifica de 1,03 para a água do mar.
Um gás está contido em um dispositivo vertical pistão-cilindro e sem atrito. O pistão tem massa de 4 kg e uma seção transversal de 35c m 2 . Urna mala comprimida acima do pistão exerce uma força de 60