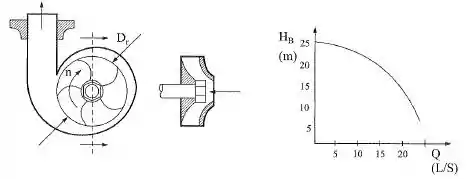
A figura mostra o esboço de uma bomba centrífuga vista em corte. Numa bomba centrífuga, a carga manométrica aumenta ao dificultar a passagem do fluido, isto é, a vazão. Isso significa que a mesma bomba, em diferentes instalações hidráulicas, pode fornececer vazões e cargas manométricas diferentes, dependendo da dificuldade criada ao escoamento do fluido. A figura mostra a curva característica de uma bomba centrífuga, cujo diâmetro do rotor é 15 cm e cuja rotação é 3500 rpm. Lembrando que os adimensionais característicos de uma bomba são e , já que, em geral, o efeito da viscosidade é desprezível e, portanto, não há necessidade levar em conta Re, determinar:
a) a curva universal para todas as bombas semelhantes à bomba dada;
b) a curva característica de uma bomba semelhante à dada, que tenha o dobro do diâmetro e a metade da rotação.
Passo 1
Vamos começar a letra a) analisando os adimensionais para a bomba na situação dada:
Agora vamos substituir os valores conhecidos nas duas equações:
Usando essas duas relações é possível determinar a curva univrsal para as bombas semelhantes a dada no enunciado.
Passo 2
Agora para a letra b) sabemos que:
Dessa forma, a partir dos adimensionais:
Podemos isolar e e deixa-los em função dos adimensionais:
Substituindo os valores conhecidos:
Passo 3
Agora, para obter a curva dessa bomba, vamos descobrir o valor dos adimensionais do passo 1 para os pontos plotados no gráfico do enunciado, então temos:
Agora, pegando esse conjunto de valores e substituindo nas equações do passo 1, conseguimos encontrar os adimensionais:
Para os pontos então, temos:
Agora vamos pegar esses valores e substituir nas equações para e para a bomba protótipo:
O conjunto de pontos será:
Podemos observar que permaneceu igual, enquanto houve mudança em , plotando esses resultados em um gráfico, temos:
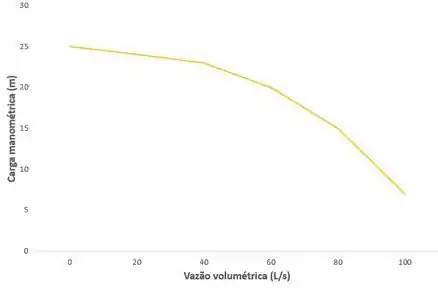
Resposta
Ei, a resposta está no passo a passo :)