Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 1.Problemas - Ex. 17

A aceleração de aeronaves de alta velocidade algumas vezes é expressa em múltiplos de (múltiplos da aceleração da gravidade padrão). Determine a força líquida para cima, em , que um homem de sofrerá numa aeronave cuja aceleração é de .

Passo 1

O enunciado que saber qual vai ser a força vertical resultante aplicada sobre um homem que é acelerado a para cima. Ou seja, a aeronave empurra o homem e faz ele se deslocar com uma aceleração vezes maior que a aceleração da gravidade . A figura acima mostra os dados que o enunciado fornece para a gente conseguir calcular .

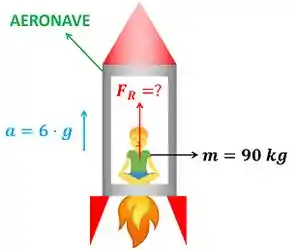
é a massa do homem.

No próximo passo vamos aprender a calcular .

Passo 2

Para calcular essa força resultante para cima, nós temos que utilizar a segunda lei de Newton.

No entanto, a aceleração vale . Logo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema de fornecimento de líquido está sendo criado de forma que o etileno glicol escoe por um orifício na parte inferior de um tanque grande, como mostra a Figura P7-87. Os projetistas precisam p

Você precisará dos resultados do Problema 7-59 para resolver este problema. Uma minúscula partícula de aerossol cai com velocidade terminal constante V. O número de Reynolds ésuficientemente pequeno p

Combine os resultados dos Problemas 7-58 e 7-59 para gerar uma equação para a velocidade terminal V de um partícula de aerossol que cai no ar (Figura). Certifique-se de que o seu resultado é consisten

Repita o Problema 7-85, exceto por um parâmetro dependente diferente: o tempo necessário para esvaziar o tanque, t v a z i o . Gere uma relação adimensional para t v a z i o como função dos seguintes

Repita o Problema 7-48, mas não assuma que o tanque é grande. Em vez disso, considere o diâmetro do tanque D t a n q u e e a profundidade média do líquido h t a n q u e como parâmetros adicionais rele