Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 158
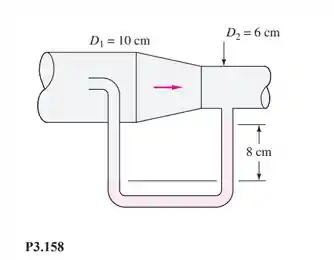
Na Figura P3.158, o fluido que escoa é CO2 a 20°C. Despreze as perdas. Se e o fluido manométrico é o óleo Meriam vermelho (), calcule (a) e (b) a vazão volumétrica do gás, em m3/h.
Passo 1
Bom, vamos começar encontrando o valor de . Para encontrar este valor basta fazer o cálculo da pressão hidrostática entre os pontos A e B que estão representados na imagem aí em baixo (lembrando que é dito para as perdas serem negligenciadas):
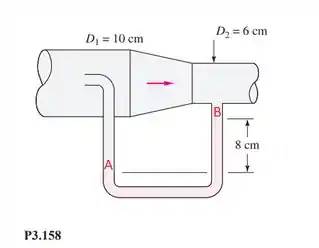
Bora lá então:
A densidade do óleo foi dada em densidade relativa , então devemos multiplicar pela densidade da água (lembrando que o sistema está a 20°C) para encontrar :
Para a densidade do gás carbônico, vamos precisar recorrer a equação dos gases ideais, já que o sistema se encontra a 20°C (293 K) e considerando que na pressão sobre o sistema o CO2 é um gás. A massa molar do CO2 é e a constantes do gases é . Agora é só substituir:
A altura em metros é e a aceleração da gravidade . Substituindo essa galera na equação:
Vale ressaltar que , já que podemos falar que a pressão em A é a mesma que a pressão em 1 e a pressão em B é a mesma que a pressão em 2, sendo 1 e 2 os pontos abaixo:
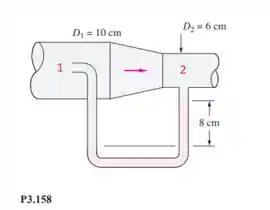
Sendo assim:
E como já falei , ou seja, fizemos a letra “a” da questão.
Passo 2
Na letra “b” precisamos encontrar , e isto é simples, basta aplicar bernoulli entre os pontos 1 e 2, mas, antes de tudo, vamos lembrar que os dois pontos estão na mesma altura, ou seja, os termos referentes à altura se anularam e que o ponto 1 lê a pressão de estagnação, ou seja, nesse ponto a velocidade é zero (). Com isso na cuca bora aplicar na equação:
Vale lembrar que a densidade na equação de bernoulli se refere à densidade do fluido que escoa pelo tubo, que no nosso caso é o CO2. Substituindo os dados e fazendo as continhas:
Passo 3
Para acharmos a vazão basta fazer:
Onde é a velocidade e é a área da seção transversal. Como o exercício pede a vazão volumétrica no tubo, vamos usar . A área da seção transversal no ponto 2 pode ser escrita (lembrando que o diâmetro nesta região é ):
Agora é só substituir na equação da vazão:
Lembrando que a questão pede esse valor em m3/h, então (só multiplicar por 3600):
Resposta
Letra a) e letra b) .