O diâmetro de um tanque de água cilíndrico é e sua altura é . O tanque é enchido com água e está aberto para a atmosfera. Um orifício de diâmetro com uma entrada uniforme (ou seja, sem perdas) e aberto na parte inferior. Desenvolva uma relação para o tempo necessário para que o tanque (a) esvazie até a metade e (b) esvazie completamente.
Passo 1
Bom, vamos ver como isso fica em forma de diagrama (até porque facilita nossa vida ):
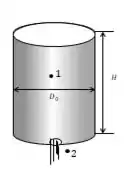
Para determinarmos a vazão, precisamos primeiramente saber qual é a velocidade, como não há componentes complexos a serem tratados, podemos aplicar a equação de Bernoulli!
Passo 2
Pelo nosso diagrama, podemos dizer que ambos os ponto e tem contato com a atmosfera, logo, . Além, disso, a velocidade no ponto é aproximadamente , uma vez que o tanque é largo em relação a saída. Por fim, o ponto é de referência, ou seja, .
A partir da nossa analise, podemos substituir na equação:
Certo, agora como podemos achar o tempo como variável? Através da vazão que relaciona a altura com o tempo!
Passo 3
A vazão volumétrica é a área multiplicada pela velocidade (). Assim, podemos expressar a quantidade de água saindo durante um instante de tempo através da derivação:
A massa que sai é igual a que está dentro do tanque, pelo fato de esvaziar, ocorre uma diminuição de nível:
Igualando as expressões e substituindo as variáveis, temos:
Isolamos o :
Assim, podemos transformar em integral. Para isso, vale lembrar que o nosso intervalo de tempo é e a altura , logo:
Resolvendo isso:
Passo 4
Quando queremos que o tanque esvazie até a metade, quer dizer que e , logo
E, para o item (b), esvaziando completamente, temos que e :
Prontinho!!
Resposta
(a)
(b)