Ao viajar em uma estrada suja, a parte inferior de um carro atinge uma pedra e um pequeno furo aparece na parte inferior do tanque de gasolina. Se altura da gasolina no tanque for de , determine a velocidade inicial da gasolina no orifício. Discuta como a velocidade mudará com o tempo e como o escoamento será afetado se a tampa do tanque estiver hermeticamente fechada.
Passo 1
Bom gente, aqui nós temos um problema no tanque de gasolina que é atingido por uma pedra, assim, precisamos determinar a velocidade inicial da gasolina no carro.
Para resolvermos, podemos usar a equação de Bernoulli, uma vez que nessa situação não temos componentes que causariam perdas por atrito.
Agora, vamos observar o esquema e fazer uma análise:
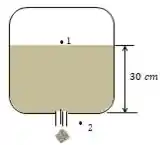
O ponto é exposto à superfície da gasolina assim como o ponto é exposto a atmosfera, logo, . A velocidade no ponto é aproximadamente , uma vez que o tanque é largo em relação a saída. As alturas serão e (nosso ponto de referência).
Passo 2
A partir da nossa analise, podemos substituir na equação:
Substituindo os dados do enunciado, temos:
Portanto, a velocidade irá diminuir com o tempo e isso se deve ao nível de gasolina no tanque, o qual irá reduzir. Por fim, se a tampa do tanque estiver completamente fechada, não haverá nenhum ar acima do nível do combustível. Logo, a pressão se reduz e a velocidade também!!
Resposta
;
A velocidade irá diminuir à medida que o nível de gasolina se reduz. Com a tampa do tanque fechada, não haverá nenhum ar acima do nível do combustível. Logo, a pressão se reduz e a velocidade também.