Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 41

Um tanque pressurizado de água tem um orifício de 10   c m de diâmetro na parte inferior, onde a água é descarregada para a atmosfera. O nível da água está 3   m acima da saída. A pressão do ar do tanque acima do nível da agua é de 300   k P a (absoluta) enquanto a pressão atmosférica é de   100   k P a . Desprezando os efeitos do atrito, determine a vazão de descarga inicial da água do tanque.

Passo 1

Bom, vamos ver como isso fica em forma de diagrama (até porque facilita nossa vida ):

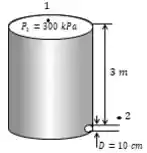
Para determinarmos a vazão, precisamos primeiramente saber qual é a velocidade, como não há componentes complexos a serem tratados, podemos aplicar a equação de Bernoulli!

Passo 2

Pelo diagrama, nós temos um ponto 1 com um determinado valor de pressão e o ponto 2 que entra em contato com a atmosfera, logo, P 2 = P a t m . Alem disso, a velocidade no ponto 1 é aproximadamente V 1 ≅ 0 , uma vez que o tanque é largo em relação a saída. Por fim, tomando o ponto 2 como referencia, temos a altura z 2 = 0 .

Substituindo isso na equação do nosso amigo Bernou:

P 1 ρ g + V 1 2 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2

P 1 - P 2 ρ g + z 1 = V 2 2 2 g

Isolamos a velocidade:

V 2 = 2 ( P 1 - P 2 ) ρ + 2 g z 1

Passo 3

Substituindo os dados do enunciado na nossa expressão do Passo 1 , temos:

V 2 = 2 × ( 300 × 10 3 - 1 00 × 10 3 ) 1000 k g m 3 + 2 × 9,8 m s 2 × 3   m

V 2 = 400 + 2 94 5 = 21,42 m s

A vazão volumétrica é a área multiplicada pela velocidade, em se tratando do nosso cilindro, temos

v ˙ = π D 2 4 × V 2

Logo,

v ˙ = π 0,1   m 2 4 × 21,42 m s = 0,168 m 3 s

Prontinho!!

Resposta

0,168 m 3 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bocal está acoplado na ponta de uma mangueira de incêndio com diâmetro interno D = 75m m . O bocal é de perfil liso e tem diâmetro de saída d = 25m m . O bocal foi projetado para operar com uma pre
O campo de velocidade para um dipolo plano é dado na Tabela 6.2. Se ∧ = 3m 3 . s - 1 , a massa específica do fluido é ρ = 1,5k g / m 3 e a pressão no infinito é 100 kPa, trace um gráfico da pressão ao
Um velho truque de mágica é feito com um carretel vazio e uma carta de baralho. A carta é apoiada contra o fundo do carretel. Contrariamente à intuição, quando alguém sopra para baixo através do orifí
Um objeto, com superfície inferior plana, move-se para baixo com velocidade U = 1,5m / s dentro do jato de líquido do Problema 4.81. Determine a pressão mínima de suprimento necessária para produzir o
Um jato de ar, horizontal e assimétrico, com 10 mm, de diâmetro, atinge um disco vertical de 190 mm de diâmetro. A velocidade do jato é 69 m/s na saída do bocal. Um manômetro é conectado ao centro do