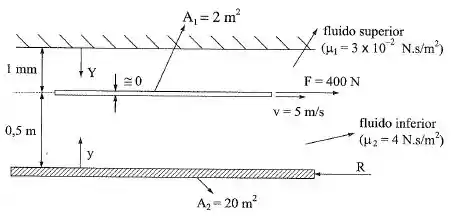
Na figura, uma placa de espessura desprezível e área desloca-se com constante, na interface de dois fluidos, tracionada por uma força . Na parte superior, e o diagrama de velocidades é considerado linear. Na placa inferior, o diagrama é dado por . Pede-se:

1. A tensão de cisalhamento na parte superior da placa em movimento;
2. A tensão de cisalhamento na face inferior da mesma placa;
3. A expressão do diagrama de velocidades no fluido superior;
4. A expressão do diagrama de velocidades no fluido inferior ;
5. A força que mantém a placa da base em repouso.

Para calcularmos a tensão na parte inferior podemos utilizar a seguinte relação:

Temos então que encontrar , que pode ser descrita como:

Logo:

A expressão para a velocidade em função de , por se tratar de um sistema linear, é dada por:

Podemos substituir as condições iniciais para encontrarmos os coeficientes:

Logo:

Temos também que:

Logo:

Portanto:

Na região do fluido inferior o sistema se comporta como uma parábola, logo:

Substituindo as condições iniciais, temos que:

Logo:

Temos também que:

Logo:

Outra relação que pode nos dar uma equação é a de que:

Como , temos que, no ponto :

Logo:

Resolvendo o sistema por substituição, temos que:

Logo:

A velocidade na parte inferior da placa será dada pela equação:

A força que mantem a base em repouso pode ser encontrada a partir da sua respectiva tensão de cisalhamento no ponto.

Temos que:

Logo: