Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 47

Um eixo com 6,00   c m de diâmetro está sendo empurrado axialmente para o interior de um mancal com 6,02   c m de diâmetro e 40   c m de comprimento. A folga, considerada uniforme, é preenchida com óleo cujas propriedades são ν =   0,003   m 2 / s e d =   0,88 . Calcule a

força necessária para puxar o eixo a uma velocidade constante de 0,4   m / s .

Passo 1

Primeiro vamos fazer um esquema da nossa questão para ilustrar nosso problema:

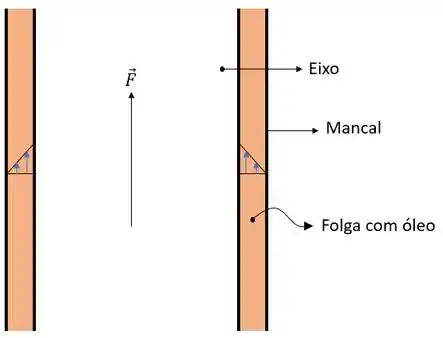
Nossa questão nos pede a força F necessária para manter o eixo a uma velocidade de 0,4   m / s , vamos pôr a mão na massa!

Passo 2

Agora que tal assumirmos que a distribuição de velocidade na folga é linear?

Desta forma nossa força é balanceada pela resistência a tensão de cisalhamento do óleo, assim temos:

F = τ A p a r e d e = μ ⋅ V Δ R ⋅ π D i L = ρ v V π D i L R e - R i

Que tal substituirmos nossos coeficientes por valores numéricos? Vamos lá!

F = 0,88 ⋅ 998   k g m 3 ⋅ 0,003 m 2 s ⋅ 0,4   m s ⋅ π ⋅ 0,06   m ⋅ 0,4   m 0,0301 - 0,0300   m

F = 794,61   N

Isso é tudo pessoal, essa foi rápida! \o/

Resposta

F = 794,61   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Operfildevelocidadedacamada­limiteviscosa,mostradonaFig.2.15,podeseraproximadoporumaequaçãocúbica:Acondiçãolimiteéu=U(avelocidadedacorrentelivre)nabordalimiteθ(ondeoatritoviscososetornazero).Determine
A água é normalmente considerada como um fluido incompressível quando se avaliam variações na pressão estática. Na verdade, a água é 100 vezes mais compressível que o aço. Considerando que o módulo de
Qual é o número de Reynolds da água a 20°C escoando a 0,25 m/s através de tubo de diâmetro 5 mm? Se agora o tubo for aquecido, a que temperatura média da água irá ocorrer a transição do escoamento par
De acordo com Folsom [6], a elevação capilar Δh (mm) de uma interface água­ar em um tubo é correlacionada pela seguinte expressão empírica: Δ h=A e - b D noqualD(mm)éodiâmetrodotubo,A=0,400eb=4,37.Voc
Operfildevelocidadedacamada­limiteviscosa,mostradonaFig.2.15,podeseraproximadoporumaequaçãoparabólica:Acondiçãolimiteéu=U(avelocidadedacorrentelivre)nabordalimiteθ(ondeoatritoviscososetornazero).Deter