Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 14

For the three-liquid system shown, compute h1 and h2.

Neglect the air density

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Desenhando o esquemático para o sistema de três líquidos contendo água, mercúrio e óleo. O sistema consiste de três tubos verticais com base A , B e C em níveis iguais:

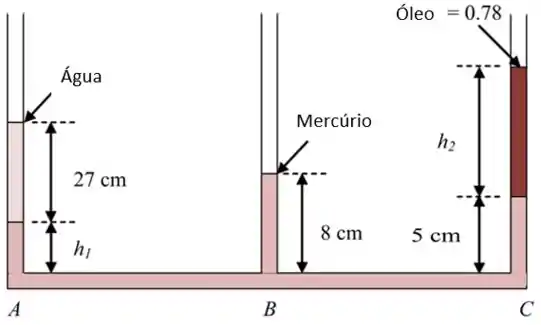
Passo 2

Da tabela de propriedades de líquidos comuns

Densidade da água: ρ á g u a = 998   k g / m 3

Densidade do mercúrio: ρ m e r c ú r i o = 13550   k g / m 3

Calculando a densidade de peso da água

γ á g u a = ρ á g u a g

Aqui, g é a aceleração devido a gravidade

Substituindo valores

γ á g u a = 998 ⋅ 9,81

→ γ á g u a = 9790   N / m 3

Passo 3

Calculando a densidade de peso do mercúrio

γ m e r c ú r i o = ρ m e r c ú r i o g

Aqui, g é a aceleração devido a gravidade

Substituindo valores

γ m e r c ú r i o = 13550 ⋅ 9,81

→ γ m e r c ú r i o = 132925,5   N / m 3

Passo 4

Calculando o peso de densidade do óleo

γ ó l e o = ρ ó l e o g = S G γ á g u a

Aqui, a gravidade específica do óleo é S G

Substituindo valores

γ ó l e o = 0,78 ⋅ 9790

→ γ ó l e o = 7636,2   N / m 3

Passo 5

Todos os três tubos são abertos pra atmosfera. Então, não tem pressão manométrica no topo dos tubos.

A pressão é igual nos pontos A , B e C

Considerando a pressão nos pontos A e B

P A = P B

→ 0,27 γ á g u a + γ m e r c ú r i o h 1 = 0,08 γ m e r c ú r i o

Resolvendo para h 1

h 1 = 0,08 γ m e r c ú r i o - 0,27 γ á g u a γ m e r c ú r i o

Substituindo valores

h 1 = 0,08 ⋅ 132925,5 - 0,27 ⋅ 9790 132925,5

∴ h 1 = 6   c m

Resposta

h 1 = 6   c m

Exercícios de Livros Relacionados

Enuncie a lei de Pascal e dê um exemplo do mundo real para ela.
Explique por que algumas pessoas têm sangramento do nariz e outras sentem falta de ar em grandes altitudes.
A leitura de um medidor de vácuo conectado a uma câmara é de 24k P a em um local onde a pressão atmosférica é de 92k P a . Determine a pressão absoluta na câmara.
Qual é a diferença entre pressão manométrica e pressão absoluta?
Alguém diz que a pressão absoluta de um líquido de densidade constante dobra quando a profundidade dobra. Você concorda? Explique.