Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 115
The 2-in by 2-in by 12-ft spar buoy from Fig. P2.113 has
5 lbm of steel attached and has gone aground on a rock, as
in Fig. P2.115. Compute the angle θ at which the buoy will
lean, assuming that the rock exerts no moments on the spar.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Deixe o comprimento submerso do esporão ser . Encontre o volume do esporão.
Encontre o volume da parte submersa do esporão.
Encontre o peso do esporão.
Aqui, é a gravidade específica da água do mar, e é o peso específico da água do mar.
O peso atua para baixo a partir do ponto
Passo 2
Encontre a força de empuxo que atua na haste. Peso da água deslocada
Substituindo valores
Esta força de flutuabilidade atua para cima a partir do ponto .
Como o peso do aço é , a flutuabilidade devido ao aço é , a força de reação atuando sobre o aço da rocha é e o peso e flutuabilidade do aço atua ao longo do ponto
Passo 3
O diagrama de corpo livro da haste é
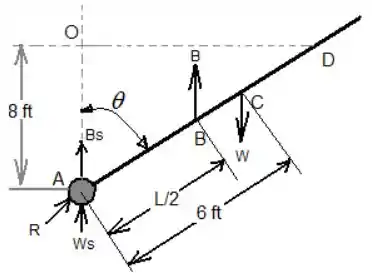
Passo 4
Tome o impulso sobre o ponto .
Substituindo os valores
Do diagrama, encontre o ângulo de inclinação.
Substituindo valores
Portanto, o ângulo de inclinação é .