Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 38

Ar forçado a 25 °C e 10 m/s é usado para resfriar componentes eletrônicos montados sobre uma placa de circuito impresso. Considere um chip com 4 mm de comprimento e 4 mm de largura, localizado a 120 mm da aresta frontal. Como a superfície da placa é irregular, o escoamento é perturbado e a correlação de convecção apropriada possui a forma N u x = 0,04 R e x 0,85 P r 0,33 .

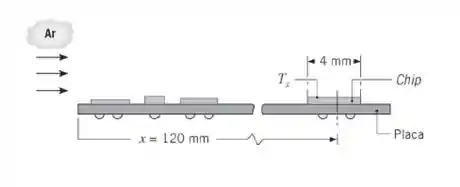
Estime a temperatura da superfície do chip, T s , se a sua taxa de dissipação de calor for de 30 mW.

Passo 1

Nesse exercício, nós vamos considerar um coeficiente de convecção médio sobre o comprimento do chip como sendo igual ao coeficiente de convecção no centro do mesmo. Então, sabendo que o calor por convecção no chip é dado por:

q c = h - c A s T s - T ∞

Isolando a temperatura superficial do chip, chegamos em:

q c h - c A s = T s - T ∞ → T s = q c h - c A s + T ∞

Só que nós precisamos da temperatura superficial para pegar as propriedades do ar para calcular Nusselt e Reynolds, então vamos chutar uma temperatura inicial de 45 °C, sendo assim, a temperatura média será:

T - = T s + T ∞ 2 = 45 + 25 2 → T - = 35   ° C

Então, agora, como temos T - = 35   ° C = 308   K , podemos aproximar essa temperatura para 310 K para ficar mais fácil encontrar as propriedades de interesse. Dessa forma, recorrendo à tabela A.4 do apêndice A, para essa temperatura, temos as seguintes propriedades:

k = 0,027   W / m . K

ν = 16,9.10 - 6   m 2 / s

P r = 0,706

Passo 2

Então, de acordo com o que assumimos no passo 1 para o coeficiente convectivo, vamos então calcular o número de Nusselt para um ponto no centro do chip, então, com a relação dada no enunciado, temos:

N u x = 0,04 R e x 0,85 P r 0,33

Então precisamos calcular o número de Reynolds para o centro do chip. Lembrando da fórmula para o número de Reynolds, temos:

R e x = V x ν

Substituindo os valores conhecidos e o ponto x = 120   m m , temos:

R e x = 10 0,12 16,9.10 - 6 → R e x = 71005,92

Agora podemos substituir os valores conhecidos na equação para Nusselt, onde teremos:

N u x = 0,04 71005,92 0,85 0,706 0,33 → N u x = 474

Passo 3

Agora, sabendo que o coeficiente convectivo é dado por:

h x = N u x k x o

Substituindo os valores conhecidos, chegamos em:

h x = 474 0,027 0,12 → h x = 106,7   W / m 2 . K

Então agora podemos retornar à equação para a temperatura superficial descrita lá no passo 1 e substituir os valores conhecidos, então, teremos:

T s = q c h - c A s + T ∞ = 30.10 - 3 106,7 4.10 - 3 2 + 25 → T s = 42,6   ° C

Resposta

T s = 42,6   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mercúrio líquido a 250°C está escoando na velocidade de 0,3 m/s em paralelo ao longo de uma placa plana de 0,1 m de comprimento, onde há um comprimento inicial sem aquecimento de 5 cm. A seção aquecid
Repita o problema 7-37 para um local com altidade de 1610 m onde a pressão atmosférica é de 83, 4 KPa
Uma série de transitores de potência dissipando 5 W cada deve ser resfriada em uma placa de alumínio quadrada de 25 cm x 25 cm com um ventilador soprando ar a 35°C a uma velocidade de 4 m/s. A tempera
Placas paralelas formam um coletor solar que cobre um telhado, como mostrado na figura abaixo. As placas são mantidas a 15ºC, enquanto o ar ambiente a 10ºC escoa ao longo do telhado com V = 4 m/s. Det
Ar a 1 atm e 20°C está escoando sobre a superfície superior de uma placa plana fina de 0,5 m de comprimento. A velocidade de escoamento do ar é de 50 m/s, e a temperatura da superfície da placa é mant