Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 39
Ar a pressão atmosférica e a uma temperatura de 25 °C escoa paralelamente, com velocidade de 5 m/s, sobre uma placa plana com 1 m de comprimento que é aquecida com um fluxo térmico uniforme de 1250 W/m². Suponha que o escoamento seja turbulento ao longo de todo o comprimento da placa.
(a) Calcule a temperatura da superfície da placa, (L), e o coeficiente convectivo local, (L), na aresta de saída, x = L.
(b) Calcule a temperatura média da superfície da placa, .
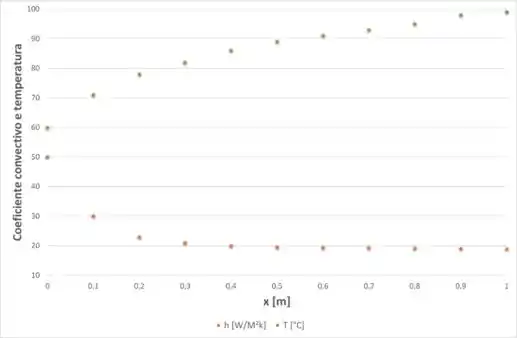
(c) Represente graficamente a variação da temperatura da superfície, (x), e do coeficiente convectivo, (L), com a distância no mesmo gráfico. Explique as características principais dessas distribuições.
Passo 1
Tá legal! Vamos começar a letra (a) assumindo uma temperatura , com isso, vamos recorrer à tabela A.4 do apêndice A para encontrar as propriedades de interesse do ar, então, teremos:
Agora, sabemos que a equação da taxa de calor transferido por convecção entre a placa e o ambiente pode ser escrita como:
No entanto, na letra (a), estamos interessados na temperatura e coeficiente convectivo na aresta de saída, em , então, a equação acima se torna:
Isolando a temperatura superficial dessa equação, temos:
Beleza! Como o enunciado nos disse que temos escoamento turbulento, então, o número de Nusselt será dado pela equação 7.46 vista nessa seção, que nos dá:
Passo 2
Então, agora precisamos calcular o número de Reynolds na posição de interesse, em x = L. Lembrando da fórmula para o número de Reynolds, temos:
Substituindo os valores conhecidos e o ponto , temos:
Então, calculando o número de Nusselt em x = L, temos:
Então, sabendo que o número de Nusselt pode ser escrito em função do coeficiente convectivo através da seguinte equação:
Substituindo os valores de interesse em , conseguimos encontrar o coeficiente convectivo nesse ponto, então, temos:
E, com esse valor, podemos retornar à equação da temperatura superficial encontrada lá no passo 1 substituir os valores conhecidos, então, teremos:
Passo 3
Agora, para a letra (b), como nós temos a temperatura no final da placa, podemos calcular a temperatura média através da seguinte equação:
Agora, vamos substituir a expressão para a diferença de temperaturas, que vimos no passo 1, então a equação se torna:
E, sabendo que o coeficiente convectivo pode ser escrito em função do número de Nusselt, conforme vimos no passo 2, a equação acima se torna:
Agora, sabemos que o número de Nusselt pode ser escrito de acordo com a relação vista no passo 1, então temos:
E, por fim, substituindo a expressão para Reynolds, chegamos na seguinte equação:
Observe que não podemos simplesmente simplificar os expoentes de e resolver a integral, pois o número de Prandtl e o coeficiente de condução dependem da posição da placa. Então essa integral só pode ser resolvida com o auxílio de um programa computacional (EES por exemplo). Então, colocando essa equação no software e os valores conhecidos, chegamos em:
Passo 4
Agora, para a letra (c), nós temos que representar a variação da temperatura da superfície e a variação do coeficiente convectivo local no mesmo gráfico, para isso, vamos utilizar as equações já vistas nesse exercício. Para a temperatura da superfície iremos utilizar:
E, para o coeficiente convectivo local, temos a relação com Nusselt, dada por:
E, substituindo a expressão para Nusselt, temos:
E, agora, substituindo a expressão para Reynolds e isolando o coeficiente convectivo, temos:
Então, calculando os valores para essas duas expressões e plotando no mesmo gráfico, temos:
