Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 77

Um forno cúbico, com 2 m de lado, é usado para tratar termicamente uma placa de aço. A superfície superior do forno é formada por aquecedores elétricos radiantes que têm uma emissividade de 0,8 e são alimentadas por uma potência de 1,5 × 10^5 W. As paredes laterais são construídas com um material refratário isolado termicamente, enquanto a base é a placa de aço, que tem uma emissividade de 0,4. Admita um comportamento de superfície cinza e difusa para o aquecedor e a placa, e considere condições nas quais a placa está a 300 K. Quais são as temperaturas correspondentes na superfície do aquecedor e nas paredes laterais?

Passo 1

Vamos lá!!! Fazendo um esqueminha do que o enunciado ta dizendo, temos isso daqui:

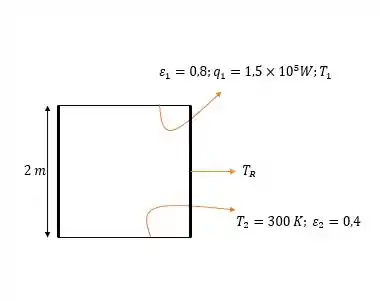
Lembrando que isso é um cubo, todos os lados são iguais!!!

E queremos descobrir T 1 e T R , se as paredes são isoladas, podemos usar:

q 1 = σ ( T 1 4 - T 2 4 ) 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 A 1 F 1 R + 1 A 2 F 2 R - 1 + 1 - ε 2 ε 2 A 2

Passo 2

Mas a gente tem q 1 , o que a gente quer é T 2 !! Lembrando que A R = A 1 = A 2 = 2 m × 2 m = 4   m , podemos isolar T 1 da seguinte forma:

T 1 = T 2 4 + q 2 A 1 σ × 1 - ε 1 ε 1 + 1 F 12 + 1 F 1 R + 1 F 2 R - 1 + 1 - ε 2 ε 2 1 4

Para achar F 12 vamos usar a figura 13.4 :

Y L = 2 2 = 1 ; X L = 2 2 = 1

Achamos F 12 = 0,2 , pela regra da soma:

F 1 R = 1 - 0,2 = 0,8

Pela regra da simetria:

F 1 R = F 2 R

Lembrando que σ = 5,67 × 10 - 8 W / m 2 K 4 :

T 1 = 300 4 + 1,5 × 10 5 4 × 5,67 × 10 - 8 × 1 - 0,8 0,8 + 1 0,2 + 1 0,8 + 1 0,8 - 1 + 1 - 0,4 0,4 1 4

Calculando:

T 1 = 1228   K

Passo 3

Agora queremos saber a temperatura da superfície isolada, T R !! Vamos fazer um balanço da radiação:

q R = q 3 = 0 = E b 3 - J 1 1 A 1 F 1 R + E b 3 - J 2 1 A 2 F 2 R

Como A 1 = A 2 e F 1 R = F 2 R :

E b 3 = J 1 + J 2 2

Sabendo que :

E b 3 = σ T 3 4

E daqui que vai sair a temperatura!!!

Substituindo e isolando T 3 :

T 3 = J 1 + J 2 2 σ 1 4

Passo 4

Mas primeiro precisamos conhecer J 1 e J 2 !! Sabendo que:

q i = E b i - J i 1 - ε i ε i A i

Isolando J i :

J i = E b i - q i A i 1 - ε i ε i      

Substituindo para achar J 1 e J 2 :

J 1 = 5,67 × 10 - 8 × 1228 4 - 1,5 × 10 5 4 × 1 - 0,8 0,8 = 1,196 × 10 5   W / m 2

J 2 = 5,67 × 10 - 8 × 300 4 - - 1,5 × 10 5 4 × 1 - 0,4 0,4 = 0,567 × 10 5   W / m 2

Podemos achar T R :

T R = 1,196 + 0,567 × 10 5 2 × 5,67 × 10 - 8 1 4

Calculando:

T R = 1117   K

Uhuuul!!

Resposta

T 1 = 1228   K

T R = 1117   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um recinto constituído por cinco superfícies. Quantos fatores de forma envolvem a geometria? Quantos desses fatores de forma podem ser determinados pela aplicação das regras da reciprocidade
O que é o método das linhas cruzadas? Para qual tipo de geometria esse método é aplicável?
O que são regra da adição e regra da superposição para fatores de forma?
64 – Três grandes barras cilíndricas de diâmetro D = 20 mm estão para ser termicamente tratadas em um forno. As barras estão inicialmente a uma temperatura de 300 K, enquanto que as paredes do forno e
58 – Um pistão sem atrito de diâmetro Dp = 50 mm, espessura δ = 10 mm, e densidade ρ = 8000 kg/m3 é colocado em um cilindro vertical de comprimento total L = 100 mm. O cilindro é perfurado em um mater