Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 82a
Uma parede composta é feita com duas grandes placas separadas por folhas de isolamento refratário, como mostrado na figura. No processo de instalação, as folhas de espessura L = 50 mm e condutividade térmica k = 0,05 W/(m · K), são separadas em intervalos de 1 m por espaços de largura w = 10 mm. As placas quente e fria têm temperaturas e emissividades T1 = 400°C, ε1 = 0,85 e T2 = 35°C, ε2 = 0,5, respectivamente. Suponha que as placas e o isolante sejam superfícies difusas e cinzas.
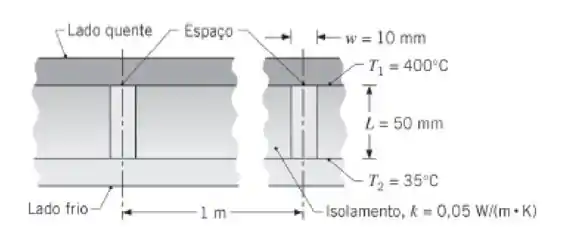
- Determine a perda térmica por radiação através do espaço por unidade de comprimento da parede composta (normal à página).
Passo 1
Vamos láa!
No desenho do livro é como se estivessimos olhando uma parede de cima e o que a gente quer é a perda de calor através desses pequenos espaços que não tem isolamento!
Vamos então olhar um esqueminha simplificado do que ta acontecendo:
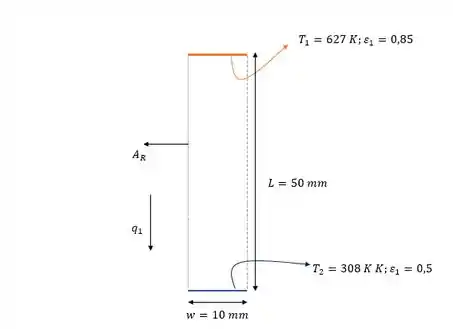
As superfícies laterais são isoladas, então:
Mas queremos a perda por unidade de comprimento, então:
Sabendo que:
E lembrando que :
Só precisamos conhecer os fatores de forma pra poder descobrir qual é a nossa perda!
Passo 2
Para descobrir vamos usar a tabela :
Temos as seguintes relações:
Calculando:
Pela regra da soma:
Por simetria:
Passo 3
Awee, podemos achar :
Lembrando que
Calculando:
Aweeee!!!