Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 91

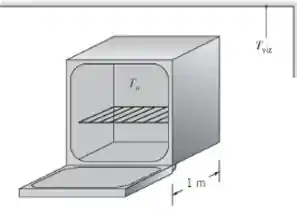
Um forno de laboratório tem uma câmara interna cúbica com 1 m de lado, com superfícies interiores com emissividade ε = 0,85. Determine a taxa de transferência de calor radiante inicial para o laboratório, no qual o forno encontra-se colocado, quando sua porta está

aberta. As temperaturas do forno e da vizinhança são Tf = 375°C e Tviz =20°C, respectivamente. Trate a porta do forno como uma superfície e as cinco paredes internas restantes do forno como outra.

Passo 1

Animados para seguir turminha ??

Como o problema nos disse nós temos duas superfícies, certo? A superfície 1 será a porta e a 2 será a parte interna do forno, agora a vizinhança nós trataremos como 3.

O problema nos pediu para achar a potência, ou seja, transferência de calor pelo forno, certo?

Para a taxa de radiação liquida transferida em uma superfície podemos usar a seguinte relação:

q i = E b i - J i 1 - ε i ε i A i = ∑ j = 1 3 J i - J j 1 A i F i j

Onde E b i é a potência emissiva, J i a radiosidade, A i a área e ε i a emissividade da superfície i.

Vamos dar uma olhada nas equações abertas?

q 1 = E b 1 - J 1 1 - ε 1 ε 1 A 1 = J 1 - J 2 1 A 1 F 12 + J 1 - J 3 1 A 1 F 13

q 2 = E b 2 - J 2 1 - ε 2 ε 2 A 2 = J 2 - J 1 1 A 2 F 21 + J 2 - J 3 1 A 2 F 23

Nós já sabemos que:

ε 1 = ε 2 = 0,85

As áreas também nós conseguimos achar fácil, já que a superfície 2 possui 5 vezes a área da tampa, não é?

A 2 = 5 A 1

Agora o que nós precisamos é achar as radiosidades e os fatores de forma !

Como a superfície 3, o ambiente, por ser um recipiente grande no qual estão inseridos os objetos, ele irá se comportar como corpo negro, ou seja:

J 3 = E b 3 = σ T 3 4

Lembrando que:

σ = 5,67 × 10 - 8   W m 2 K 4

T 1 = T 2 = 375 ° C + 273 = 648   K

T 3 = 20 ° C + 273 = 293   K

Então:

J 3 = 5,67 × 10 - 8   W m 2 K 4 293   K 4 = 417,9   W m 2

Também podemos aproveitar e calcular a potência emissiva para a superfície 1 e 2:

E b 1 = E b 2 = 5,67 × 10 - 8   W m 2 K 4 648   K 4 = 9997   W m 2

Então nós precisamos dos fatores de forma para conseguirmos calcular as radiosidades !!

Passo 2

O fator de forma do interior do forno (2) até o ambiente (3) pode ser encontrado usando a seguinte ideia, a radiação que sai do interior e atinge a porta do forno ou os arredores deve passar pela abertura, não é?

Por isso é importante nós conhecermos o fator de forma da abertura, que vamos colocar como o subscrito o .

Sabendo que:

F o 2 = 1

Podemos usar a reciprocidade e achar:

F 2 o = A o F o 2 A 2

A área da abertura é igual a área da porta:

F 2 o = 1 5 = 0,2

Vamos guardar esta informação, ok?

Olhando a Tabela 13.2 e o desenho nós obtemos:

X = Y = Z = 1   m

H = W = 1   m

Substituindo:

F 12 = 0,2

Com esta informação nós achamos mais dois fatores !! Fazendo a soma para a superfície 1:

F 13 = 1 - F 1 2 = 1 - 0,2 = 0,8

E novamente pela reciprocidade:

F 21 = A 1 F 12 A 2 = 0,2 5 = 0,04

Usando a soma:

F 13 = 1 - F 12 = 1 - 0,2 = 0,8

Já que a radiação deve passar pela abertura:

F 2 o = F 2 1 + F 2 3

F 23 = 0,2 - 0,04 = 0,16

Colocando tudo na tabela para resumir tudo que achamos:

Passo 3

Agora nós vamos substituir tudo nas equações do Passo 1:

9997   - J 1 1 - 0,8 5 0,8 5 = J 1 - J 2 1 0 , 2 + J 1 - 417,9 1 0 , 8

9997   - J 1 1 - 0,85 0,85 = J 2 - J 1 1 0 , 04 + J 2 - 417,9 1 0 , 16

Resolvendo as duas equações simultaneamente:

J 1 = 8840 W m 2

J 2 = 9728 W m 2

Agora podemos calcular a taxa de calor que chega no laboratório será a soma das duas taxas de calor que deixas as superfícies 1 e 2, ok?

q l a b o r a t o r i o = - A 1 F 1 3 J 1 - J 3 - A 2 F 2 3 J 2 - J 3

= - 1 m 2 0,8 8840 W m 2 - 9728 W m 2 + 5 m 2 0,16 9728 W m 2 - 417,9 W m 2

q l a b o r a t o r i o = - 1,42 × 10 4   W

O que acharam desta? Gostosa, não foi ?!

Resposta

q l a b o r a t o r i o = - 1,42 × 10 4   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um recinto cônico de altura h e diâmetro da base D. Determine o fator de forma a partir da superfície lateral cônica para um furo de diâmetro d localizado no centro da base.
Dois cilindros paralelos infinitamente longos, de diâmetro D, estão localizados a uma distância s um do outro. Determine o fator de visão F 12 entre esses dois cilindros.
Repita o Problema 13-19 com L = D .
Determine os fatores de forma F 13eF 2 3 entre as superfícies retangulares mostradas na Fig. P13–8.
Considere um recinto cilíndrico cuja altura é duas vezes o diâmetro de sua base. Determine o fator de forma da superfície lateral deste recinto cilíndrico para sua superfície da base.