Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 16
Dois cilindros paralelos infinitamente longos, de diâmetro D, estão localizados a uma distância s um do outro. Determine o fator de visão entre esses dois cilindros.
Passo 1
Então galerinha, vamos continuando por aqui!!
Quando nós temos superfícies infinitamente longas poderemos usar o método de linhas:
Se nós olharmos dois cilindros de frente:
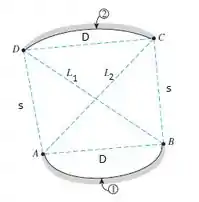
Assim o fator de forma ficará como:
Como nós temos um triângulo retângulo formado entre as linhas cruzadas e :
E a distancia de A até B é o comprimento do semi-círculo:
Substituindo:
E finalizamos mais umaaa!!
Resposta
Exercícios de Livros Relacionados
Considere a cavidade com três superfícies mostrada na figura. A placa inferior (A1) é um disco negro com 200 mm de diâmetro que é alimentado por uma taxa térmica de 10.000 W. A placa superior (A2), um
Considere duas grandes superfícies paralelas, cinzas e difusas, separadas por uma pequena distância. Se a emissividade das superfícies é de 0,8, qual deve ser a emissividade de uma barreira de radiaçã
13.56 Determine as temperaturas em regime estacionário de duas barreiras de radiação colocadas em um espaço onde há vácuo entre dois planos infinitos a temperaturas de 600 e 325 K. Todas as superfície
A extremidade de um tanque cilíndrico no espaço, que contém um propelente criogênico líquido, deve ser protegida da radiação externa (solar) pela colocação de uma fina barreira metálica em frente ao t
13.52 Um dispositivo eletrônico dissipando 50 W é fixado à superfície interna de um recipiente cúbico isotérmico, que tem 120 mm de lado. O recipiente está posicionado na maior área de serviço do ônib