Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 87

A garrafa de champanhe (d = 0,96) da Figura P2.87 está sob pressão, como mostra a leitura do manômetro de mercúrio. Calcule a força líquida sobre a extremidade hemisférica de 50 mm de raio no fundo da garrafa.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.6 do livro, chamada “Forças sobre superfícies curvas”.

Pra entender o problema, vamos olhar esse esquema abaixo:

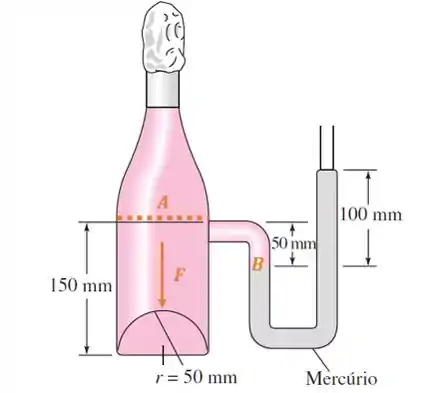
Queremos calcular a força F sobre a extremidade hemisférica de raio 50   m m , que é unicamente vertical devido à geometria simétrica da garrafa.

Para isso,primeiro iremos calcular a pressão na seção A a partir das equações de cálculo de pressão estática.

Então, vamo lá resolver essa questão juntos nos próximos passos!

Passo 2

Primeiro, vamos calcular a pressão da seção A . Para isso, devemos analisar a figura no Passo 1.

Podemos definir a pressão no ponto B ( P B ) de duas maneiras a partir das equações de estática:

P B = P a t m + ρ M g h 1

P B = P A + ρ c h g h 2

Sendo P a t m = 0 a pressão atmosférica, ρ M = 13600   k g / m ³ a massa específica do mercúrio; g = 9,81   m / s ² a aceleração da gravidade; h 1 = 100   m m = 0,1   m ; P A a pressão na seção A que queremos descobrir; ρ c h = 960   k g / m ³ a massa específica de champanhe; e h 2 = 50   m m = 0,05   m .

Combinando as equações, temos:

P A =   ρ M g h 1 - ρ c h g h 2 = 13600 k g m 3 9,81 m s 2 0,1   m - 960 k g m 3   9,81 m s 2 0,05   m

P A = 12870   N / m ²

Passo 3

Agora vamos calcular a força F a partir do seguinte balanço de forças:

F = P A A A + W c i l i n d r o - W h e m i s f é r i o

Vamo entender essa equação que eu coloquei ali em cima. Ela nos diz que a força hidrostática F é igual à força da pressão na seção A mais o peso real do líquido, ou seja o peso esperado se fosse um cilindro completo menos o peso da seção do hemisfério.

Abrindo a equação, temos:

F = P A A A + ρ c h g π R 2 L - ρ c h g 2 π R 3 3

Devemos pontuar que A A , a área na seção A , ou seja, a área da seção transversal do cilindro é π R ² . Além disso, temos π R ² L como o volume do cilindro e 2 π R 3 3 o volume da região hemisférica.

Substituindo os valores nas equações:

F = 12870 N m 2 π ( 0,05   m ) ² + ( 9,81 m s 2 ) 960 k g m 3 π 0,05   m 2 0,15   m - 960 k g m 3 2 π 0,05   m 3 3

F = 101   N + 8,62   N = 109,62   N

Pronto, matamos a questão juntos!

Resposta

A força líquida sobre a extremidade hemisférica de 50 mm de raio no fundo da garrafa é F = 109,62   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em líquidos “macios” (módulo de elasticidade volumétrica β baixo), pode ser necessário levar em conta a compressibilidade do líquido em cálculos hidrostáticos. Uma relação aproximada da massa específi
A válvula de retenção abaixo cobre uma abertura com diâmetro de 22,86 cm em uma parede inclinada. A articulação está a 15 cm da linha de centro, como mostrado. A válvula abrirá quando o momento na art
A comporta ABC na Figura P2.98 tem um quarto de círculo com 2,4 m de largura normal ao papel. Calcule as forças hidrostáticas horizontal e vertical sobre a comporta e a linha de ação da força resultan
O painel curvo BC da Figura P2.96 é um arco de 60°, perpendicular ao fundo em C. Se o painel tiver 4 m de largura, calcule a força hidrostática resultante da água sobre o painel.
Uma esfera de 0,6 m de diâmetro, pesando 1.780 N, fecha um furo de 0,3 m de diâmetro no fundo do tanque da Figura P2.99. Calcule a força F necessária para desalojar a esfera do furo.