Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 98
A comporta ABC na Figura P2.98 tem um quarto de círculo com 2,4 m de largura normal ao papel. Calcule as forças hidrostáticas horizontal e vertical sobre a comporta e a linha de ação da força resultante.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.6 do livro, chamada “Forças sobre superfícies curvas”.
Pra entender a questão, dá uma olhada na figura do enunciado. Temos uma comporta no formato de um arco de círculo, com um raio de e uma largura (imagina isso como uma terceira coordenada que “entra” dentro do papel) .
A questão quer da gente as componentes horizontal () e vertical () da força hidrostática que age sobre a comporta, além da linha de ação da força resultante.
Nos próximos passos, eu vou te mostrar como calcular essas forças e a linha de ação. Então, vamo lá resolver essa questão juntos!
Passo 2
Primeiro, vamos calcular a componente horizontal . Para isso, devemos imaginar uma projeção em um ângulo de 90° com relação à direção dessa força, como na figura abaixo:
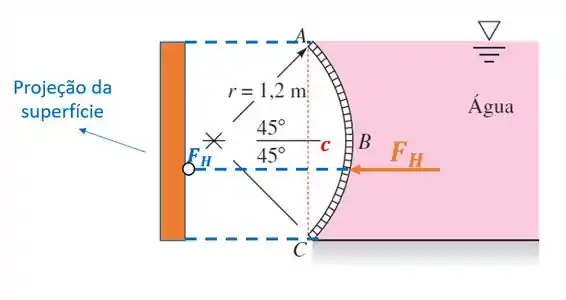
Observe que essa projeção é na verdade um retângulo, de base e altura .
Essa altura é a chamada corda do segmento circular, que é dada pela fórmula . Portanto, seu valor é:
e
Sabendo disso, podemos definir a equação para calcular a componente vertical da força hidrostática:
Sendo: o peso específico, que para água à temperatura ambiente é 9790 ; a distância do centro de massa com relação à superfície livre, que para um retângulo é metade da altura do retângulo; e a área do retângulo projetado.
Dessa forma, temos:
Passo 3
Agora vamos calcular a componente vertical .
Nesse caso, ela poderá ser calculada a partir da do que se chama peso da água “ausente”, ou seja, o peso que a água exerceria se o segmento de círculo estivesse preenchido com o fluido. A força age justamente de maneira a compensar esse peso ausente.
Pra entender melhor, veja a figura aí embaixo:
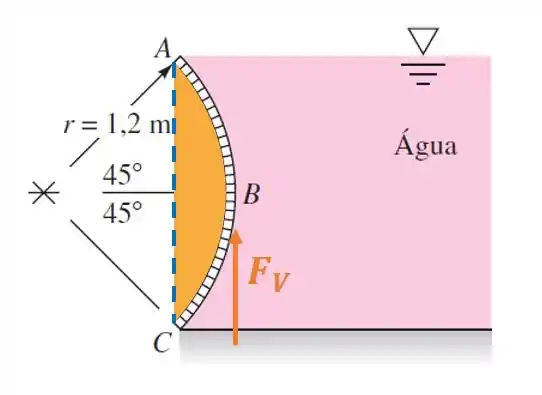
Note que para este tipo de aplicação, a componente vertical da força hidrostática irá apontar para cima.
Para prosseguir com nossos cálculos, iremos precisar calcular a área do segmento de círculo . Para isso, considere a imagem abaixo:
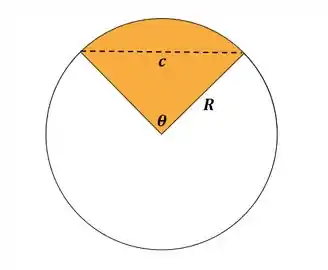
Seja o raio do segmento de círculo e é o comprimento da corda. Para a comporta do problema, sabemos que .
Dessa maneira, a área , por definição, é calculada como:
Agora sim, podemos calcular :
Passo 4
E pra finalizar a questão, iremos calcular a resultante da força hidrostática e sua linha de ação.
Primeiro, com as duas componentes e encontradas nos Passos 2 e 3, podemos calcular uma resultante a partir do módulo dessas componentes:
Fazendo uma simples relação trigonométrica com o triângulo, podemos encontrar a resultante do ângulo entre (eixo horizontal) e :
Ou seja, a linha de ação da força faz um ângulo de com a horizontal, passando pelo ponto .
Pronto, matamos a questão juntos!
Resposta
As componentes horizontais e verticais da força resultante foram, respectivamente, e .
A força hidrostática resultante é , com sua linha de ação fazendo um ângulo de com a horizontal passando pelo ponto .