Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 12
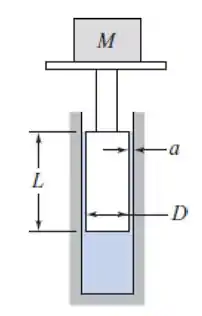
Uma grande massa é suportada por um pistão de diâmetro e comprimento . O pistão está assentado em um cilindro fechado no fundo. A folga entre a parede do cilindro e o pistão é preenchida com óleo SAE 10 a 20°C. O pistão desliza lentamente devido ao peso da massa, e o óleo é forçado a sair à taxa de . Qual é o valor da massa (em kg)?
Passo 1
Tá legal, podemos tratar esse exercício como sendo um escoamento laminar com gradiente de pressão entre placas estacionárias e paralelas, e dessa forma, utilizar a equação 8.6c vista nesse capítulo, então, temos:
De forma que o perímetro será:
Em que é o diâmetro do pistão, então, substituindo essa expressão na equação anterior e isolando a diferença de pressão, temos:
Então, sabemos que a variação de pressão será a força aplicada ao pistão divido pela sua área de seção transversal, então, temos:
Passo 2
Agora, para encontrar a diferença de pressão utilizando a equação vista no passo 1, precisamos pegar as propriedades do óleo à temperatura dada no enunciado no apêndice A, então, teremos:
Então, agora, substituindo os valores conhecidos na equação da diferença de pressão obtida no passo 1, temos:
Passo 3
Com o valor da diferença de pressão encontrada no passo 2, podemos retornar a segunda equação para a diferença de pressão encontrada no passo 1:
Sabemos que a força aplicada ao pistão, nesse caso, será o peso da massa , então, teremos:
Então, substituindo os valores conhecidos, temos: