Reconsidere o Problema 8-66. Para drenar o tanque mais rapidamente, uma bomba é instalada próxima à saída do tanque. Determine quanta entrada de potência de bomba é necessária para estabelecer uma velocidade média da água de 4 m/s quando o tanque está cheio até Z = 2 m. Considere também que a velocidade de descarga permaneça constante e estime o tempo necessário para drenar o tanque. Alguém sugere que o fato da bomba estar localizada no início ou no final do tubo não faz diferença, e que o desempenho será igual em ambos os casos, mas outra pessoa argumenta que a colocação da bomba perto do final do tubo pode causar cavitação. A temperatura da água é , de modo que a pressão do vapor d'água é e o sistema está localizado no nível do mar. Investigue se há possibilidade de cavitação e se devemos nos preocupar com a localização da bomba.
Passo 1
Oi pessoal, tudo bem?
Primeiramente, para o problema, assumimos que:
1. O fluxo é uniforme e incompressível.
2. O tubo de drenagem é horizontal.
3. O fluxo é turbulento para que o valor tabulado do coeficiente de perda pode ser usado.
4. O fator de atrito permanece constante (na realidade, muda desde que o velocidade de fluxo e, portanto, o número de Reynolds muda).
5. O efeito do fator de correção da energia cinética é desprezível, portanto definimos α = 1.
O coeficiente de perda é para uma entrada com arestas vivas. (Tabela 8-4). E o enunciado informa que o fator de atrito . O enunciado informa também que a velocidade é de 4 m/s e temos que para a temperatura de : .
O esboço do problema pode ser mostrado como:
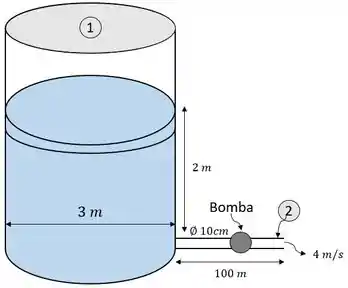
Passo 2
Tomamos o ponto 1 na superfície livre do tanque e o ponto 2 na saída do orifício.
Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:
Também tomamos o nível de referência na linha central do orifício () e assumimos a direção positiva de z para cima. Observando que o fluido em ambos os pontos é aberto para a atmosfera (e, portanto, ) e que a velocidade do fluido na superfície livre é muito baixa (), a equação de energia (Eq. 1) para um volume de controle entre esses dois pontos simplifica a:
E sabendo que a perda de carga total, agora, é definido pela soma da perda de carga maior e a perda de carga menor, assim:
Letra a) Já que o diâmetro do sistema de tubulação é constante podemos substituir e observar que a velocidade de descarga inicial é de 4 m / s, então, sabendo que:
Como sabemos todos os valores das variáveis da eq. 3, podemos encontrar a perda de carga da bomba ( ) através da eq. 2:
Portanto, a entrada de potência da bomba pode ser encontrada por:
Portanto, a bomba deve fornecer 3,52 kW de energia mecânica à água. Observe que a potência do eixo da bomba deve ser maior que isso para explicar a ineficiência da bomba.
Passo 3
Quando a velocidade de descarga permanece constante, a vazão da água se torna:
Agora, para encontrar o volume do tanque:
E o tempo necessário para drenar o tanque:
Observe que a bomba reduz o tempo de descarga de 38,9 minutos para 7,5 minutos. A suposição de velocidade de descarga constante pode ser justificada com base na cabeça da bomba ser muito maior que a cabeça de elevação (portanto, a bomba dominará processo de descarga). A resposta obtida assume que a elevação se eleva constante a 2 m (em vez de diminuindo para zero eventualmente) e, portanto, prediz o tempo real de descarga.
Passo 4
Agora, tomamos a bomba como o volume de controle, com o ponto 1 na entrada e o ponto 2 na saída.
Assumimos a entrada da bomba e os diâmetros de saída sejam os mesmos e a diferença de elevação entre a entrada da bomba e a saída seja insignificante. Então temos . A bomba está localizada perto da saída do tubo e, portanto, a pressão de saída da bomba é igual à pressão na a saída do tubo, que é a pressão atmosférica, . Além disso, pode levar , pois os efeitos de atrito e perdas bomba são contabilizadas pela eficiência da bomba.
Então a equação de energia para a bomba (eq. 1) reduz para:
Sabendo que e isolando o :
O que é impossível (a pressão absoluta não pode ser negativa). A resposta para a pergunta é que a cavitação irá ocorre porque a pressão cai abaixo da pressão de vapor de 4,246 kPa.
Resposta
Portanto: ; .