Uma grande placa de espessura encontra-se a uma temperatura uniforme , quando é subitamente imersa em um banho líquido com temperatura . A transferência de calor para o líquido é caracterizada pelo coeficiente convectivo .
(a) Com correspondendo ao plano central da placa, em coordenadas , esboce as distribuições de temperaturas para as seguintes condições: condição inicial , condição de regime estacionário e dois tempos intermediários.
(b) Em coordenadas , esboce a variação com o tempo do fluxo térmico em .
(c) Sendo , qual é o fluxo térmico em e ? Sendo a condutividade térmica da placa igual , qual é o gradiente de temperatura correspondente em ?
(d) Considere uma placa de espessura , com massa específica e calor específico . Fazendo um balanço de energia na placa, determine a quantidade de energia, por unidade de área superficial da placa , que é transferida para o banho ao longo do tempo necessário para que o regime estacionário seja atingido.
(e) De outras considerações, sabe-se que durante o processo de resfriamento por imersão o fluxo térmico em e decai exponencialmente com o tempo de acordo com a relação, , na qual está em segundos, . Use essa informação para determinar a energia por unidade de área superficial da placa que é transferida para o fluido durante o processo de resfriamento por imersão.
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional, logo a troca de calor só ocorre em uma direção, vamos fazer nosso diagrama pra facilitar nossa vida.
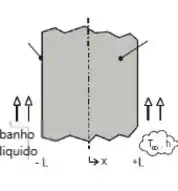
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a) Primeira coisa a se ressaltar é que ele pede em dois tempos intermediários, então vamos imaginar que mergulhamos nossa placa duas vezes em sequência assim vamos ter troca de calor em dois estados, nosso gráfico fica assim?
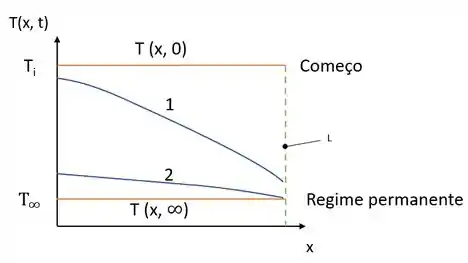
A linha que tem curva mais acentuada apresenta o primeiro mergulho, enquanto a outra com uma curva tímida apresenta o segundo mergulho no banho.
Passo 3
(b) Bem nosso problema nos pede uma representação gráfica da distribuição de temperatura ao longo da superfície, vamos calcular nossa
Integrando duas vezes em função de e temos:
Como não existe geração de calor e , eventualmente nosso gradiente de temperatura vai se tornar constante.
No regime permanente nosso fluxo vai ser dado por:
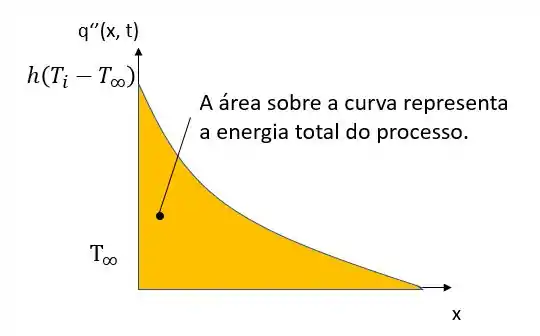
Passo 4
(c) Vamos lá! o fluxo na superfície em será o máximo e será regido pela equação:
Sendo e temos:
Agora como , temos:
Passo 5
(d) A energia gasta até chegarmos no nosso regime permanente pode ser encontrado pelo balanço de energia, que é regido pela equação , assim temos.
Como a não há energia entrando na placa, somente a dissipação de calor temos:
Passo 6
(e) A energia transferida da placa pro banho durante o processo será a área da curva apresentada na letra , assim nós podemos calcular por integral que fica assim:
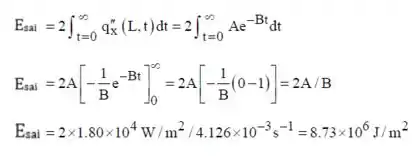
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)