O sistema unidimensional, mostrado na figura, tem massa , propriedades constantes, não apresenta geração de calor em seu interior e encontra-se inicialmente a uma temperatura uniforme . O aquecedor elétrico é subitamente energizado, fornecendo um fluxo térmico uniforme na superfície . A fronteira em , bem como todas as demais fronteiras
do sistema, encontram-se perfeitamente isoladas.
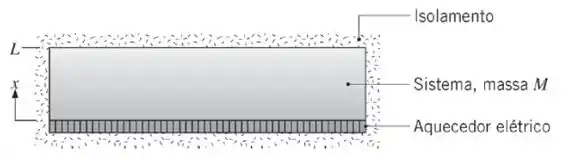
(a) Escreva a equação diferencial e identifique as condições inicial e de contorno que poderiam ser usadas para determinar a temperatura em função da posição e do tempo no sistema.
(b) Em coordenadas , esboce as distribuições de temperaturas para a condição inicial e para vários outros instantes de tempo após o aquecedor ser energizado. Uma distribuição de temperaturas em estado estacionário será atingida em algum instante?
(c) Em coordenadas , esboce o fluxo térmico nos planos , e em função do tempo.
(d) Após haver transcorrido um intervalo de tempo desde a energização do aquecedor, a sua alimentação elétrica é desligada. Considerando que o isolamento térmico é perfeito, após certo tempo o sistema finalmente atingirá uma temperatura final uniforme . Desenvolva uma expressão que permita determinar em função dos parâmetros e das características do sistema e (a área superficial do aquecedor).
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional, logo a troca de calor só ocorre em uma direção, tem uma temperatura inicial, e só recebe calor somente sobre uma superfície enquanto as demais estão isoladas.
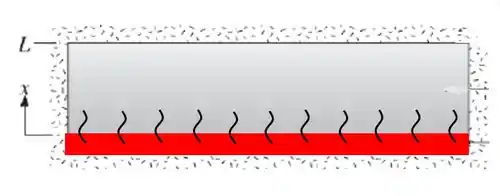
Origem e sentido da transmissão de calor.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Tendo tudo isso em mente vamos a nossa letra (a), que nos pede as condições de contorno e a nossa equação diferencial. Para isso vamos escrever nossa lei de Fourier (equação ).
Como nossa condução é unidimensional e não há geração de energia, temos:
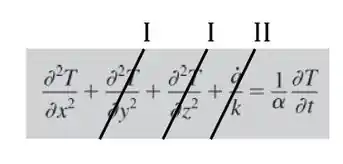
Assim nossa equação fica:
Como quanto nosso aquecedor está desligado nossa temperatura é , assim nossa equação fica:
Agora pra nossas condições de contorno, na superfície contraria ao aquecedor, não tem fluxo de calor, já que está isolada. Na outra superfície o fluxo de calor vai ser máximo, ou seja:
Passo 3
b) Pra gente esboçar o gráfico vamos fazer intuitivamente como ele faz no exemplo do livro... (até porque fica impraticável resolver e ele nem quer isso... rs)
Mas vamos usar as nossas condições de contorno.
Mas isso significa que a derivada de T em x=L é igual a zero, né??? Então a reta tangente vai ser horizontal...
E a outra:
Que nos diz que em x=0:
Então a derivada de T em x=0 vai ser sempre negativa. Então a reta tangente vai ter inclinação negativa.
Se liga só no gráfico:
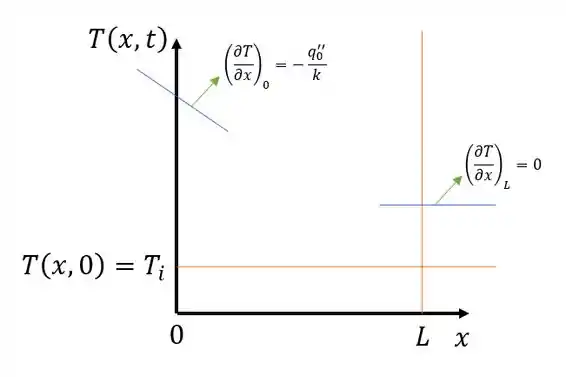
Mas a gente tendo essas tangentes aí o gráfico que cabe nessas características é esse aqui:
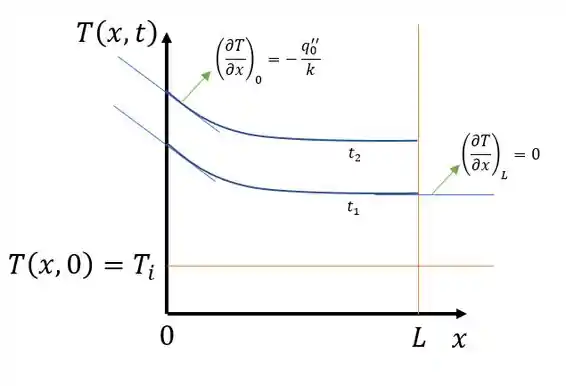
Repara que conforme vai aumentando, vai se afastando mais de .
O estado estacionário não será atingido pois a energia acumulada é igual a energia que entra, já que não tem “fuga de energia”, como a energia que entra é constante. Não existirá estado estacionário.
Passo 4
(c) Vamos lá seguindo a lógica do nosso gr��fico passado, temos:
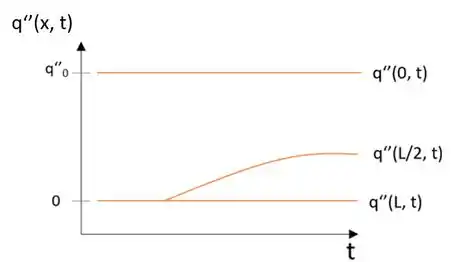
Para o instante nosso aquecedor está desligado, como a superfície está isolada não temos fluxo de calor.
Após isso nosso aquecedor é ligado, a superfície em contato imediato com ele tem fluxo constante , já em o fluxo sobe lentamente até ficar constante.
Passo 5
(d) Se nosso aquecedor for ligado e desligado após um tempo o sistema eventualmente atingirá uma temperatura constante , vamos fazer o balanço de energia pro sistema usando a equação , assim temos:
Assim temos que:
Organizando nossa equação temos:
Isso é tudo pessoal! \o/
Resposta
Ei, a resposta está no passo a passo :)