Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 97
Hidrocarboneto líquido entra em um tubo de de diâmetro e de comprimento. A temperatura de entrada do líquido é , e a temperatura da parede do tubo é de . As propriedades médias do líquido são , e . Para vazão de , a temperatura de saída do líquido é medida a . Estime a temperatura de saída do líquido quando a vazão for reduzida para . Dica: Para transferência de calor em tubos. no escoamento laminar e no escoamento turbulento.
Passo 1
Dados fornecidos:
Diâmetro do tubo:
Comprimento do tubo:
Temperatura de entrada do hidrocarboneto:
Temperatura de saída do hidrocarboneto:
Temperatura da parede do tubo:
Taxa de fluxo de massa:
Taxa de fluxo de massa:
As propriedades médias do hidrocarboneto líquido:
Passo 2
Podemos fazer o seguinte diagrama esquemático do tubo:
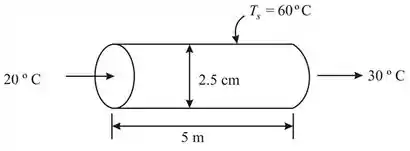
Passo 3
Primeiro, podemos determinar o coeficiente de transferência de calor a partir de um balanço energético. Assim temos:
Aqui, é taxa de fluxo de massa, é o calor específico do hidrocarboneto, é a temperatura de saída do hidrocarboneto, é a temperatura de entrada do hidrocarboneto, é a temperatura da superfície do tubo, é a média da temperatura de entrada e saída , e é a área da superfície do tubo . Assim temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 4
Vamos agora calcular o número de Reynolds para o primeiro caso. Assim temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Este valor é menor que o valor de , portanto, é um fluxo laminar.
Passo 5
Vamos agora calcular o número de Reynolds para o segundo caso. Assim temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Este valor é menor que o valor de , portanto, é um fluxo laminar.
Passo 6
Usando o a relação entre os números de Nusselt e Reynolds para o fluxo laminar dada pelo enunciado podemos escrever a seguinte relação:
Temos que pode ser escrito da seguinte forma:
e do ser escrito como:
Substituindo e na relação acima temos:
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 7
Agora, podemos determinar a temperatura de saída do hidrocarboneto a partir de um balanço energético usado no passo 3. Assim temos:
Substituindo os termos da equação pelos dados obtidos, temos:
Portanto, a temperatura de saída do hidrocarboneto é .