Um iglu é construído na forma de um hemisfério, com raio interno de 1,8 m e paredes de neve compactada com uma espessura de 0,5 m. No interior do iglu, o coeficiente de transferência de calor nas superfícies é de 6 W/(m2 · K); no lado de fora, sob condições de ventos normais, ele é de 15 W/(m2 · K). A condutividade térmica da neve compactada é de 0,15 W/(m · K). A temperatura da camada de gelo sobre a qual o iglu se encontra é de –20°C e a sua condutividade térmica é a mesma da neve compactada.
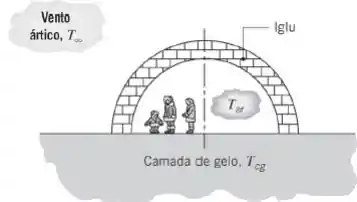
(a) Considerando que os corpos dos ocupantes do iglu forneçam uma fonte contínua de calor de no interior do iglu, calcule a temperatura do ar no seu interior quando a temperatura do ar externo é de . Certifique-se de levar em consideração as perdas de calor pelo chão do iglu.
(b) Usando o circuito térmico da parte (a), execute uma análise de sensibilidade paramétrica para determinar quais variáveis têm um efeito significativo na temperatura do ar no interior do iglu. Por exemplo, sob condições de ventos muito fortes, o coeficiente convectivo externo pode dobrar ou até mesmo triplicar. Faz algum sentido construir o iglu com paredes que tenham a metade ou então o dobro da espessura original?
Passo 1
Nessa questão nós temos um iglu construído em forma hemisférica na calota de gelo e temos a espessura da parede do iglu e os coeficientes de convecção internos/externos . Então, nosso circuito térmico é,
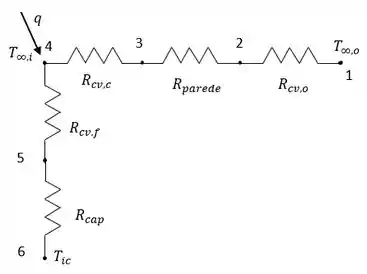
Com isso queremos encontrar a temperatura do ar interna quando a temperatura do ar externo for , assumindo que os nossos esquimós forneçam dentro do iglu.
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições de estado estacionário;
(2) O coeficiente de convecção é o mesmo no piso e no teto do iglu;
(3) O piso e o teto estão a temperaturas uniformes;
(4) A calota de gelo do piso lembra o disco em meio semi-infinito;
(5) A condução é unidimensional através das paredes do iglu.
O circuito térmico que representa a perda de calor do iglu para o ar externo e através do piso para a calota de gelo é mostrado no Passo 1 e a perda de calor é:
Passo 3
Para a convecção no teto:
Para a convecção do exterior:
Para a convecção do teto:
Para a convecção da parede:
Para a convecção do iglu:
Passo 4
O foi determinado a partir do fator de forma da Tabela 4.1. Então,