Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 3.Problemas - Ex. 50
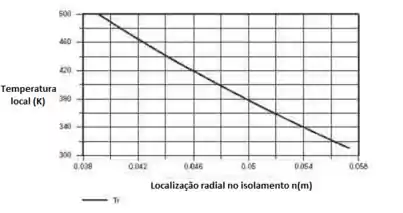
Desejamos determinar o efeito da adição à tubulação de vapor do problema anterior de uma camada de isolante à base de magnésia. Pode-se supor que o coeficiente de transferência de calor por convecção na superfície externa do isolante permanece em 25 W/(m2*K) e a emissividade é e = 0,8. Determine e represente graficamente a perda de calor por unidade de comprimento do tubo e a temperatura da superfície externa em função da espessura do isolante. Se o custo da geração de vapor é de J e a linha de vapor opera a 7000 h/ano, recomende uma espessura de isolante e determine a economia anual correspondente nos custos com energia. Represente graficamente a distribuição de temperaturas na camada de isolante com a espessura recomendada.
Passo 1
Iai gente! Prontos pra detonar mais uma questão comigo? Bora lá!
Se referindo ao circuito térmico, segue que o balanço de energia na superfície externa se define como:
Das equações do livro 3.9, 3.28 e 1.7, temos que:
Passo 2
Essa expressão pode ser resolvida para sendo uma função de e a perda de calor pode ser determinado pela determinação de qualquer um dos lados da equação de balanço de energia.
A perda de calor pode ser reduzida em até 91% por um valor de aproximadamente em em .
Passo 3
A taxa de economia relativa à energia anual por unidade de comprimento é, portanto:
E isso pode ser visualizado no esquema abaixo:
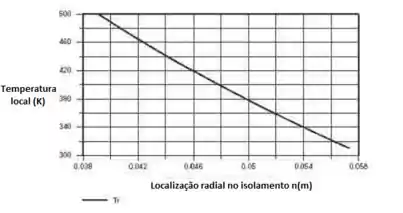
Espero que tenham curtido! Nos vemos na próxima questão, galera!
Resposta
