Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 6

An incompressible plane flow has the velocity potential

ϕ 5 2Kxy, where B is a constant. Find the stream function

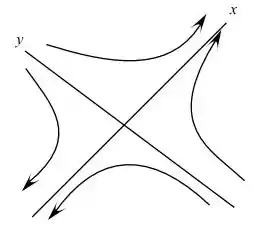
of this fl ow, sketch a few streamlines, and interpret the flow

pattern

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Escreva a equação dada.

φ = 2 B x y

Aqui, é a φ função potencial, e é a B constante. Calcule as funções de velocidade e relacione-as com a função de fluxo.

u   = ∂ φ ∂ x   = ∂ ψ ∂ y v   = ∂ φ ∂ y   = - ∂ ψ ∂ x

Aqui, φ está a função de fluxo. Substitua 2 B x y para φ .

∂ ψ ∂ y   = ∂ ( 2 B x y ) ∂ x   = 2 B y ∂ ψ ∂ x   = - ∂ ( 2 B x y ) ∂ y   = - 2 B x

Passo 2

Integrar parcialmente com relação a y e depois com relação a x .

  ∫   ∂ ψ = ∫   2 B y ⋅ ∂ y ψ = B y 2 + c   ∫   ∂ ψ = ∫   2 B x ⋅ ∂ x ψ = B x 2 + c

Escreva a solução final da função de fluxo com base nessas duas relações.

ψ   = B y 2 - B x 2 + c   = B y 2 - x 2 + c

Assim, a função de fluxo é B y 2 - x 2 + c .

Passo 3

Desenhe o diagrama simplificado a partir da equação obtida.

Resposta

ψ = B y 2 - x 2 + c

Exercícios de Livros Relacionados

Combine o escoamento de estagnação da Figura 8.19 b com uma fonte na origem: f z = A z 2 + m ⋅ ln ⁡ z Trace as linhas de corrente para m = A L 2 , sendo L uma escala de comprimento. Interprete.
Investigue o potencial complexo f z = U ∞ ( z + a 2 / z ) e interprete o padrão de escoamento.
Considere o potencial de velocidades em coordenadas polares ϕ = B r 1,2c o s ( 1,2 θ ) , sendo B uma constante. Verifique se ∇ 2 ϕ = 0 . Sendo o caso, encontre a função corrente associada ψ ( r ,θ ) ,
Use o método das imagens para construir o padrão de escoamento de uma fonte 1 m próxima a duas paredes, como mostrado na Figura P 8.72 . Esboce a distribuição de velocidades ao longo da parede inferio
Construa um sistema de imagens para calcular o escoamento de uma fonte a distâncias desiguais de duas paredes, como na Figura P 8.73 . Encontre o ponto de máxima velocidade sobre o eixo y .