Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas para exames de fundamentos de engenharia - Ex. 5

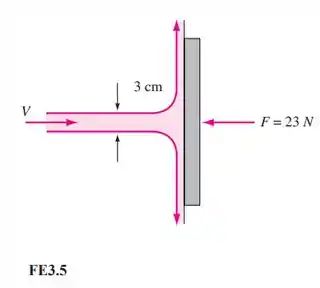
Um jato de água de 3 cm de diâmetro atinge uma placa normal, como na Figura FE3.5. Se a força necessária para escorar a placa é de 23 N, qual é a velocidade do jato?

(a) 2,85 m/s, (b) 5,7 m/s, (c) 8,1 m/s, (d) 4,0 m/s, (e) 23 m/s.

Passo 1

Esta é uma questão muito simples, só precisamos fazer uma análise das forças em x. O somatório das forças em x vai possuir apenas o termo da força necessária para placar escoar (lembrando que esta força aponta para a esquerda, logo, de acordo com nosso referencial, ela será negativa), ou seja:

Em relação ao balanço de momento, teríamos que analisar as correntes em x e em y, entretanto, se fizermos apenas em x já vamos ter o resultado final. Em x, temos apenas uma corrente que é o próprio jato.

O balanço para esse cara fica:

Agora é só juntar tudo:

Resposta

Letra B) (b) 5,7 m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.101 Um fluido incompressível escoa em regime permanente na região de entrada de um canal bidimensional de altura 2 h = 100m m e largua w = 25m m . A vazão é Q = 0,025m ³ / s ³ . Encontre a velocidad

4.102 Um fluido incompressível escoa em regime permanente na região de entrada de um tubo circular de raio R = 75m m . A vazão é Q = 0,1m ³ / s ³ . Encontre a velocidade unifrome U 1 na entrada. A dis

4.97 Água escoa em regime permanente através da curva de 90° do Problema 4.39. O escoamento na entrada está a p 1 = 185k P a (absoluta). O escoamento na saída é não uniforme, vertical e à pressão atmo

4.99 Um pequeno objeto redondo é testado em um túnel de vento de 0,75 m de diâmetro. A pressão é uniforme nas seções 1 e 2. A pressão a montante é 30 mm de H 2 O (manométrica), a pressão a jusante é 1

4.109 Quando um jato plano de líquido atinge uma placa inclinada, ele se parte em duas correntes de velocidades iguais, mas de espessuras desiguais. Para escoamento sem atrito, não pode haver força ta