Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 99

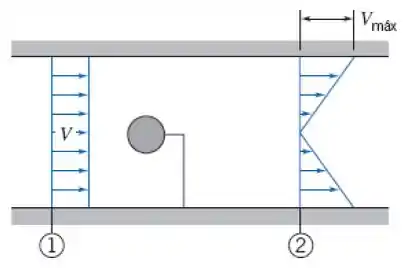
4.99 Um pequeno objeto redondo é testado em um túnel de vento de 0,75 m de diâmetro. A pressão é uniforme nas seções 1 e 2. A pressão a montante é 30 mm de H 2 O (manométrica), a pressão a jusante é 15 mm de H 2 O (manométrica) e a velocidade média do ar é 12,5 m/s. O perfil de velocidade na seção 2 é linear; ele varia de zero na linha do centro do túnel a um máximo na parede do túnel. Calcule (a) a vazão mássica no túnel de vento, (b) a velocidade máxima na seção 2 e (c) o arrasto sobre o objeto e sua haste de sustentação. Despreze a resistência viscosa na parede do túnel.

Passo 1

(a) Para calcular a vazão mássica vamos precisar da densidade do ar. Vamos assumir que esteja a temperatura ambiente e olhar o valor na Tabela A.8 no Apêndice A ( ρ = 1,19   k g / m 3 )

m ˙ = ρ V π D 2 4

m ˙ = 1,19 12,5 π 0,75 2 4 ˙

m ˙ = 6,57   k g / s

Passo 2

(b) Precisamos agora achar uma equação que descreva o perfil da velocidade em 2. Como é linear, podemos representar por:

V r = a r + b

Sabemos que V 0 = 0   e V R = V m á x (onde R = D / 2 =0,375).

0 = b

V m á x = a R + b

a = V m á x R

Então,

V r = V m á x R r

Pela equação da continuidade temos:

m ˙ = ∫ 0 R ρ V r 2 π r d r

m ˙ = ∫ 0 R ρ V m á x R r 2 π r   d r

m ˙ = ∫ 0 R ρ V m á x R 2 π r 2 d r

m ˙ = ρ V m á x 2 π r 3 3 R 0 R

m ˙ = ρ V m á x 2 π R 2 3

6,57 = 1,19 V m á x 2 π ( 0,375 ) 2 3

V m á x = 3 6,57 1,19 2 π 0,375 2

V m á x = 18,75   m / s

Passo 3

Vamos usar a componente x da equação de quantidade de movimento.

R x + p 1 A - p 2 A = V - ρ V A + ∫ 0 R V r ρ V r 2 π r d r

R x = - p 1 A + p 2 A + V - ρ V A + ∫ 0 R V m á x R r ρ V m á x R r 2 π r d r

R x = - p 1 A + p 2 A + V - ρ V A + ∫ 0 R ρ V m á x R 2 2 π r 3 d r

R x = - p 1 A + p 2 A + V - ρ V A + ρ V m á x 2 π R 2 2

Antes de substituir os valores, vamos passar as pressões para Pascal, senão dá ruim.

p 1 = ρ á g u a g h 1

p 1 = 999 9,81 0,03

p 1 = 294   P a

p 2 = ρ á g u a g h 2

p 2 = 999 9,81 0,0 15

p 2 = 147   P a

Agora sim...

R x = - 294 π 0,375 2 4 + 147 π 0,375 2 4 + 12,5   - 1,19 12,5 π 0,375 2 4 + 1,19 18,75 2 π 0,375 2 2

R x = 55,65   N

Resposta

(a) m ˙ = 6,57   k g / s

(b) V m á x = 18,75   m / s

(c) R x = 55,65   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jato de água é dirigido contra uma pá defletora, que poderia ser uma pá de turbina ou outra peça de uma máquina hidráulica qualquer. A água sai de um bocal estacionário, de 40m m de diâmetro, com u
Um jato plano de água atinge uma pá divisora, repartindo-se em duas correntes planas, conforme mostrado. Determine a razão entre as vazões mássicas, m 2 m 3 ˙ ˙ , necessária para produzir uma força re
Um carinho é propelido por um jato de líquido que sai horizontalmente de um tanque, conforme mostrado. A pista é horizontal e a resistência ao movimento pode ser desprezada. O tanque é pressurizado de
Considere uma série de pás curvas atingidas por um jato contínuo de água com velocidade constante, V = 86,6m / s . O jato sai de um bocal de 50m m de diâmetro e as pás se movem com velocidade constant
Considere novamente o jato e o carrinho do Problema 4.149, mas inclua uma força de arrasto aerodinâmico proporcional ao quadrado da velocidade do carrinho, F D = k u 2 , com k = 2,0N s 2 / m 2 . Deduz