Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 97

4.97 Água escoa em regime permanente através da curva de 90° do Problema 4.39. O escoamento na entrada está a p 1 = 185   k P a (absoluta). O escoamento na saída é não uniforme, vertical e à pressão atmosférica. A massa da estrutura do canal é M c = 2,05   k g ; o volume interno do canal é V = 0,00355   m ³ . Avalie a força exercida pelo canal sobre o duto de suprimento de água.

Passo 1

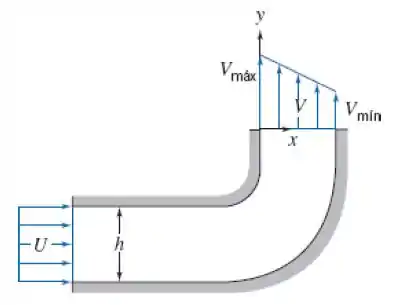
Achando a equação que descreve V:

Em x = h ,   V = V m í n .

Considerando que varia linearmente, (fazendo certa mágica, mas é pensável pois é uma reta decrescente)

V = - A x + B

Em x = 0 , V = V m á x , do outro enunciado temos V m á x = 2   V m í n , então:

:

2   V m í n = - A 0 + B

B = 2 V m í n

Em x = h ,   V = V m í n :

V m í n = - A h + 2 V m í n

A = V m í n h

Ficamos, então com:

V = 2   V m í n - V m í n h x  

Da continuidade:

U A = ∫ 0 h V h   d x

U h 2 = ∫ 0 h 2   V m í n - V m í n h x   h   d x

U h 2 = 2 V m í n x - V m í n h x 2 2 h 0 h

U h 2 = 2 V m í n h 2 - V m í n h 2 2

U h 2 = V m í n h 2 2 - 1 2

V m í n = U 3 2

V m í n = 5   m / s

Portanto,

V m á x = 10   m / s

Passo 2

Começando pela componente x da equação da quantidade de movimento:

R x + p 1 A = U - ρ U A

R x = - p 1 A + U - ρ U A

R x = - 185000 - 101000 0,0755 2 + 7,5 - 999 7,5 0,0755 2

R x = - 799   N

Mas a força exercida pelo canal sobre o duto é:

K x = - R x

K x = 799   N

Passo 3

Agora para componente y:

R y - M g - ρ g V = ∫ 0 h V ρ V h   d x

R y = M g + ρ g V + ∫ 0 h 2   V m í n - V m í n h x ρ 2   V m í n - V m í n h x h   d x

R y = M g + ρ g V + ∫ 0 h ρ V m í n 2 h 4 - 4 x h + x 2 h 2   d x

R y = M g + ρ g V + ρ V m í n 2 h 4 x - 2 x 2 h + x 3 3 h 2 0 h

R y = M g + ρ g V + ρ V m í n 2 h 4 h - 2 h + h 3

R y = M g + ρ g V + ρ V m í n 2 h 2 7 3

R y = 2,05 9,81 + 999 9,81 0,00355 + 999 5 2 0,0755 2 7 3

R y = 387   N

Mas a força exercida pelo canal sobre o duto é:

K y = - R y

K y = - 387   N

Resposta

K x = 799   N

K y = - 387   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carrinho mostrado rola com resistência desprezível. Ele deve acelerar para a direita a uma taxa constante de 2,5m / s 2 . Isso deverá ser realizado pela “programação” da velocidade do jato de água,
Considere uma pá defletora simples, com curvatura θ , movendo-se horizontalmente com velocidade constante, u , sob a ação de um jato impingente como no Problema 4.128. A velocidade absoluta do jato é
A catapulta hidráulica do Problema 4,138 é acelerada por um jato de água que atinge sua pá curva e se move ao longo de uma pista horizontal com resistência desprezível. Em um dado instante, sua veloci
A aceleração do conjunto carrinho/pá do Problema 4,128 deve ser controlada pela variação do ângulo da sua pá, θ , a partir do instante em que ele inicia o movimento. Uma aceleração constante, a = 1,5m
Um jato de água, de 100m m de diâmetro e velocidade de 3m / s para a direita é defletido por um cone que se move de encontro ao jato a uma taxa de 14m / s , conforme mostrado. Determine:a) A espessura