Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 102

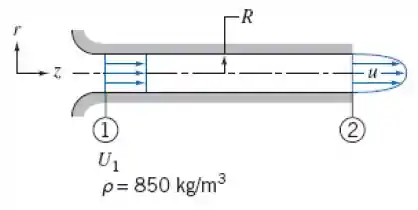
4.102 Um fluido incompressível escoa em regime permanente na região de entrada de um tubo circular de raio R = 75   m m . A vazão é Q = 0,1   m ³ / s . Encontre a velocidade unifrome U 1 na entrada. A distribuição de velocidades em uma seção a jusante é

u u m á x = 1 - y R 2

Avalie a velocidade máxima na seção a jusante. Calcule a queda de pressão que existiria no tubo, se o atrito viscoso nas paredes fosse desprezível.

Passo 1

A partir da vazão podemos achar a velocidade na entrada.

Q = U 1 A

Q = U 1 π R 2

0,1 = U 1 π 0,075 2

U 1 = 5,66   m / s

Passo 2

Da equação da continuidade temos:

Q = ∫ 0 R u m á x 1 - r R 2 2 π r   d r

Q = ∫ 0 R 2 π u m á x r - r 3 R 2   d r

Q = 2 π u m á x r 2 2 - r 4 4 R 2 0 R

Q = 2 π u m á x R 2 2 - R 4 4 R 2

Q = 2 π u m á x R 2 2 - R 2 4

Q = 2 π u m á x R 2 4

Q = π u m á x R 2 2

u m á x = 2 Q π R 2

u m á x = 2 0,1 π 0,075 2

u m á x = 11,32   m / s

Passo 3

Vamos usar a componente z da equação de quantidade de movimento para calcular a queda de pressão.

p 1 A - p 2 A = U 1 - ρ U 1 A + ∫ 0 R U 2 ρ U 2 2 π r   d r

p 1 A - p 2 A = U 1 - ρ U 1 A + ∫ 0 R u m á x 1 - y R 2 ρ u m á x 1 - y R 2 2 π r   d r

p 1 A - p 2 A = U 1 - ρ U 1 A + ∫ 0 R 2 π ρ u m á x 2 r - 2 r 3 R 2 + r 5 R 4   d y

p 1 A - p 2 A = U 1 - ρ U 1 A + 2 π ρ u m á x 2 r 2 2 - 2 r 4 4 R 2 + r 6 6 R 4 0 R

p 1 A - p 2 A = U 1 - ρ U 1 A + 2 π ρ u m á x 2 R 2 2 - R 4 2 R 2 + R 6 6 R 4

p 1 A - p 2 A = U 1 - ρ U 1 A + 2 ρ u m á x 2 π R 2 1 2 - 1 2 + 1 6

p 1 A - p 2 A = U 1 - ρ U 1 A + 2 ρ u m á x 2 A 1 6

p 1 - p 2 = U 1 - ρ U 1 + ρ u m á x 2 1 3

p 1 - p 2   = - ρ U 1 2 + ρ u m á x 2 1 3

p 1 - p 2   = - 850 5,66 2 + 850 11,32 2 1 3

p 1 - p 2 = 9077   P a

Resposta

U 1 = 5,66   m / s

u m á x = 11,32   m / s

p 1 - p 2 = 9077   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O prato circular, cuja seção reta é mostrada, tem um diâmetro externo de 0,20m . Um jato de água, com velocidade de 35m / s , atinge o prato concentricamente. O diâmetro do jato saindo do bocal é 20m
Um jato contínuo de água é empregado para propelir um carrinho ao longo de uma pista horizontal, conforme mostrado. A resistência total ao movimento do carrinho é dada por F D = k u 2 , com k = 0,92N
Água, proveniente de um bocal estacionário, atinge uma pá fixa sobre um carrinho. O ângulo da pá é θ = 120 ° . O carrinho afasta-se do bocal com velocidade constante u = 10m / s à medida que a pá rece
Um jato de óleo ( S G = 0,8 ) atinge uma lâmina curva que desvia o fluido de um ângulo θ = 180 ° . A área do jato é 1200m m 2 e sua velocidade relativa ao bocal estacionário é de 20m / s . Determine a
O prato circular, cuja seção transversal é mostrada, tem um diâmetro externo de 0,15m . Um jato de água o atinge concentricamente e em seguida escoa para fora ao longo da superfície do prato. A veloci