Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 85
Uma junta de termopar esférica, com de diâmetro, está inserida no interior de uma câmara de combustão para medir a temperatura dos produtos de combustão. Os gases quentes possuem uma velocidade de .
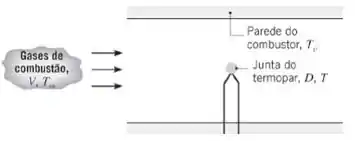
(a) Se o termopar estiver a temperatura ambiente, , quando for inserido na câmara, estime o tempo necessário para que a diferença de temperaturas,, atinja da diferença de temperaturas inicial, Despreze os efeitos da radiação e da condução através dos terminais do termopar. As propriedades da junta do termopar podem ser aproximadas por , e as dos gases de combustão por e .
(b) Se a junta do termopar possuir uma emissividade de e as paredes resfriadas da câmara de combustão estiverem a , qual é a temperatura da junta em regime estacionário, estando os gases de combustão a ? A condução através dos terminais pode ser desprezada.
(c) Para determinar a influência da velocidade do gás no erro de medida do termopar, calcule a temperatura da junta do termopar, em regime estacionário, para velocidades na faixa de . A emissividade da junta pode ser controlada através da aplicação de um fino revestimento. Para reduzir o erro de medida, deve a emissividade ser aumentada ou diminuída? Para , calcule a temperatura da junta em regime estacionário, para emissividades na faixa de .
Passo 1
Nessa questão nós temos a velocidade e temperatura dos gases de combustão. Assim como o diâmetro e emissividade da junção do termopar e a temperatura do combustível.
A partir dessas informações precisamos encontrar o tempo para atingir da elevação máxima da temperatura do termopar e a temperatura do termopar em estado estacionário. Vamos juntos resolver essa questão
Passo 2
Para resolver essa questão vamos assumir que:
(1) Há validade da análise de capacitância concentrada;
(2) As propriedades são constantes;
(3) A condução é desprezível por meio de fios condutores;
(4) A troca de radiação ocorre entre superfície pequena e um gabinete grande.
Na letra (a) queremos o tempo necessário para que a diferença de temperaturas,, atinja da diferença de temperaturas inicial, . Se a análise da capacitância concentrada puder ser utilizada, temos que:
Passo 3
Negligenciando a correlação da razão de viscosidade para efeitos de propriedades variáveis, o uso de com a correlação de Whitaker gera:
Substituindo os valores, temos:
Como,
O método de capacitância concentrada pode ser usado. Então,
Passo 4
Na letra (b) queremos a temperatura da junta em regime estacionário, estando os gases de combustão a . Fazendo um balanço de energia na junção e avaliando a troca de radiação,
Então, com ,