Bioengenharia tecidual envolve o desenvolvimento de substitutos biológicos que restauram ou melhoram a função de tecidos. Uma vez fabricados, os órgãos engenheirados podem ser implantados e crescem no interior do paciente, evitando a carência crônica de órgãos naturais que acontecem quando o transplante tradicional de órgãos é usado. A fabricação de um órgão artificial envolve duas etapas principais. Primeiramente, uma base de sustentação porosa é fabricada com tamanho e distribuição dos poros específicos, assim como forma e tamanho total. Em segundo lugar, a superfície externa da base de sustentação é semeada com células humanas que crescem no interior dos poros da base. O material da base é biodegradável e com o tempo é substituído por tecido sadio. O órgão artificial está, então, pronto para ser implantado no paciente.

As formas complexas dos poros, os tamanhos pequenos dos poros e as formas não usuais dos órgãos impedem o emprego de métodos de fabricação tradicionais para construir as bases de sustentação. Um método que tem sido usado com sucesso é uma técnica de fabricação de sólido sem forma, na qual pequenas gotas esféricas são direcionadas para um substrato. As gotas estão inicialmente fundidas e se solidificam quando colidem com o substrato a temperatura do ambiente. Pelo controle do local da deposição da gota, bases de sustentação complexas podem ser construídas, de gota em gota. Um dispositivo similar ao do Problema 7.78 é usado para gerar gotas uniformes com de diâmetro a uma temperatura inicial . As partículas são enviadas através de ar estagnado a . As propriedades da gota são e

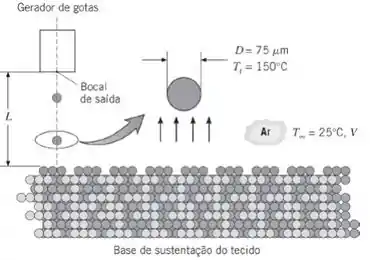
(a) É desejável que as gotas saiam do bocal na sua velocidade terminal. Determine a velocidade terminal das gotas.

(b) É desejável que as gotas colidam a estrutura a uma temperatura . Qual é a distância necessária entre a saída do bocal e a estrutura, ?

Para resolver a questão vamos assumir que a transferência de calor por radiação é desprezível, a resposta térmica de capacitância é concentrada e os efeitos de transferência de calor por microescala são desprezíveis. Além disso, as propriedades do ar vão ser retiradas da Tabela A.4, onde,

Na letra (a) nós queremos a velocidade terminal das gotas. Um equilíbrio de força na partícula gera:

Onde,

E,

Nós também sabemos que,

A velocidade correta produzirá valores de e que são consistentes com a Figura 7.9. Uma solução de tentativa e erro gera (usando propriedades em ).

Na letra (b) nós queremos a distância necessária entre a saída do bocal e a estrutura. Usando a correlação de Whitaker com as propriedades avaliadas em temos:

Então,

Tendo que,

Então,

Gerando,

A distância de separação, , é então: