Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 1.Problemas - Ex. 16
Na latitude de , a aceleração da gravidade em função da altitude acima do nível do mar é dada por , onde e . Determine a altitude acima do nível do mar onde o peso de um objeto decresce .
Passo 1
O enunciado quer saber a altitude em relação a o nível do mar que um objeto precisa estar para diminuir seu peso em . A figura abaixo mostra alguns dados que o enunciado nos deu para fazer esse cálculo.
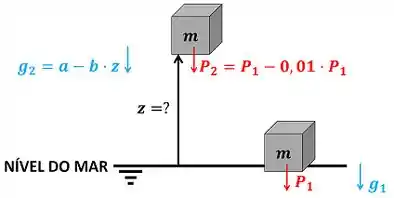
é o peso do objeto no nível do mar. é o peso do objeto, quando ele está na altitude . é a gravidade do objeto no nível do mar. é a gravidade do objeto, quando ele está na altitude . é a massa do objeto. Não vai ser necessário conhecer paa resolver a questão.
No próximo passo vamos descobrir a primeira etapa para calcular .
Passo 2
O primeiro passo para resolver esse exercício é escrever numa equação o que o enunciado falou sobre a diminuição do peso do objeto. O enunciado disse que o peso do objeto acima do nível do mar é menor o peso do objeto no nível do mar.
Passo 3
O segundo passo é substituir a fórmula dos pesos na equação acima.
A fórmula do peso é:
A fórmula do peso é:
Substituindo essas duas fórmulas na primeira equação, encontramos que:
Passo 4
O terceiro passo é substituir a fórmula das gravidades na equação anterior. Antes, temos que lembrar que a altitude do objeto, quando seu peso vale , é igual a (nível do mar) e a altitude do objeto, quando seu peso vale , é igual a .
Substituindo na equação de antes:
Passo 5
O último passo é reorganizar a fórmula acima para encontrar .