Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 163
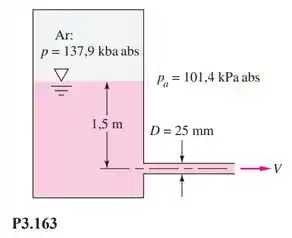
O líquido na Figura P3.163 é o querosene a 20°C. Calcule a vazão volumétrica do tanque (a) desprezando as perdas e (b) considerando perdas no tubo, .
Passo 1
Precisamos encontrar a vazão para os dois casos pedidos na questão, mas antes vamos precisar encontrar a velocidade para os dois casos.
Vamos utilizar a equação de Bernoulli:
Vamos começar resolvendo a questão desprezando as perdas no sistema ().
O nosso ponto 1 vai estar na superfície de querosene dentro do tanque e o ponto 2 no fluxo saindo do tanque, desta maneira vamos ter que e que (a gente supõe que o diâmetro do tanque é grande o suficiente para desprezar a velocidade do fluido).
Vamos chamar e sabemos que .
Com estes dados a equação de Bernoulli fica:
Lembrando de converter (provavelmente este valor de pressão dado pela questão está errado, creio que a unidade já era para estar em kPa, mas enfim).
Passo 2
No segundo caso, as perdas são dadas pela a equação .
Repetindo o processo anterior temos:
Passo 3
Agora é só encontrar as vazões, mas antes, bora encontrar a área da seção transversal do tubo de saída de fluido:
Pronto, a vazão para o caso que desprezamos as perdas é:
E para o caso em que consideramos as perdas:
Resposta
Letra a) ;
Letra b) .