Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 67
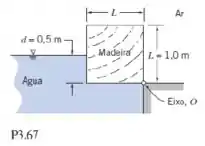
Um longo bloco de madeira, de seção quadrada, é articulado em uma de suas arestas. O bloco está em equilíbrio quando imerso em água na profundidade mostrada. Avalie a densidade relativa da madeira, se o atrito no pivô for desprezível.
Passo 1
Nesse problema temos um bloco articulado e flutuante, devemos encontrar a densidade relativa, sendo o atrito desprezível. Algumas das equações básicas que temos são:
Como todo problema da mecânica, temos que fazer algumas considerações: líquido estático; densidade constante; sem atrito na dobradiça.
Para um fluido incompressível , em que é a pressão manométrica e é medido para baixo.
A força na seção vertical é igual a de um retângulo de altura e largura .
Passo 2
Tendo essas análises, podemos calcular a força,
A localização da força é dada por:
Passo 3
A força na seção horizontal é devida à pressão constante e está no centroide, logo:
Avaliando os momentos sobre a dobradiça:
Assim, temos:
Isolando :
Prontinho!!