Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 70
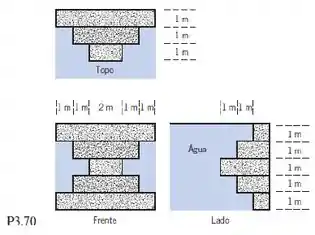
Para a geometria mostrada, qual é a força vertical da água sobre a represa?
Passo 1
Para solucionarmos esse problema temos aqui a geometria da barragem com uma força vertical. Consideramos que a agua seja estática e incompressível e, como nos pedem a força da água, todas as pressões serão escritas como medidor. Logo, as equações básicas são
Onde:
onde é a pressão manométrica e a altura é medida para baixo a partir da superfície livre.
Passo 2
A força em cada seção horizontal é, tendo em vista que: profundidade de largura ,
Observamos na figura que e mudam em termos de e para cada seção da barragem! Portanto, a força total é:
Começando de cima para baixo,
O sinal deu negativo pois a força é para cima.
Resposta
Exercícios de Livros Relacionados
Uma comporta retangular (de largura w = 2 m) é articulada conforme mostrado, com um batente na borda inferior. Em que profundidade H a comporta estará prestes a abrir?
Uma comporta plana semicircular AB, articulada ao longo de B, é suportada pela força horizontal FA aplicada em A. O líquido à esquerda da comporta é água. Calcule a força FA requerida para o equilíbri
Uma comporta plana, de espessura uniforme, suporta uma coluna de água conforme mostrado. Determine o peso mínimo da comporta necessário para mantêla fechada.
Uma seção de parede vertical deve ser construída com mistura pronta de concreto derramada entre formas. A seção de parede tem 3 m de altura, 0,25 m de espessura e 5 m de largura. Calcule a força exerc
Uma janela de acesso, na forma de um triângulo isósceles e articulada no topo, é colocada na parede vertical de uma forma contendo concreto líquido. Determine a força mínima que deve ser aplicada no p