Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 26
Um método proposto para geração de eletricidade a partir da irradiação solar é concentrar a irradiação no interior de uma cavidade que é colocada no interior de um grande recipiente de um sal com alto ponto de fusão. Se todas as perdas térmicas forem desprezadas, parte da irradiação solar que entra na cavidade é usada para fundir o sal, enquanto o restante é usado para alimentar um ciclo de Rankine. (O sal é fundido durante o dia e é ressolidificado a noite de modo a haver geração de energia nas 24 horas do dia.)
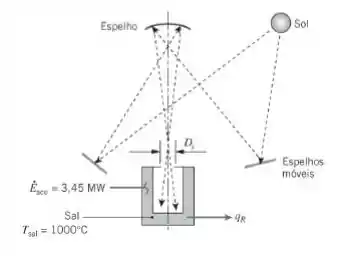
Considere condições nas quais a potência solar entrando na cavidade é de qsol = 7,5 MW e a taxa de acúmulo de energia no sal é de Ėacu = 3,45 MW. Para uma abertura na cavidade de diâmetro Ds = 1 m, determine a taxa de transferência de calor para o ciclo Rankine, qR. A temperatura do sal é mantida no seu ponto de fusão, Tsal = Tm = 1000°C. Despreze perdas térmicas por convecção e a irradiação da vizinhança
Passo 1
Vamos resolver essa questãozinha juntos, ok? Partiu!
Nosso enunciado pediu a taxa de transferência de calor para o ciclo Rankine… Vamos nessa então!
Podemos encontrar ela usando a equação:
Ops! temos que encontrar esse calor que foi perdido antes de calcular o calor que o enunciado deseja, tranquilo?
Passo 2
Pra encontrar esse , vamos usar a seguinte equação:
Passo 3
Agora sim podemos encontrar nosso calor de Rankine…
ou
Show de bola! Conseguimos!