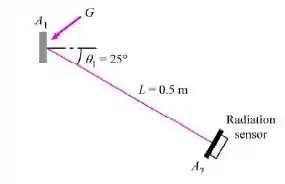
Uma pequena superfície de área A1 = 3 cm² e um sensor de radiação com área A2 = 1 cm² são orientados como mostrado na figura abaixo. A superfície A1 é opaca e mantém uma temperatura constante de T1 = 400 K. A absortividade e emissividade da superfície A1 são 0,5 e 0,7, respectivamente. Considerando que a superfície A1 está experimentando 2000 W/m² de irradiação, determine a taxa em que a radiação emitida a partir de A1 é interceptada pelo sensor.

Vamos aproximar nossas áreas como superfícies diferencias, onde o ângulo feito por A2 sendo visto de A1 é:

A radiosidade da superfície A1 é expressada como:

Lembrando que