Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 34
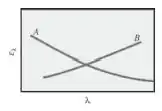
Para os materiais A e B, cujas emissividades hemisféricas espectrais variam com o comprimento de onda conforme mostrado a seguir, como a emissividade hemisférica total varia com a temperatura? Explique sucintamente.
Passo 1
Temos uma questão interpretativa e teórica, certo? Vamos lá!
Bom, a emissividade hemisférica total pode ser obtida pela equação 12.43:
E nós sabemos que o poder emissivo de um corpo negro se torna maior em menores comprimentos de onda com o aumento da temperatura. Isso nos diz que, o fator de ponderação, que é nosso:
Ele aumenta em comprimentos de onda mais baixos e diminui em comprimentos de onda mais longos com o aumento da temperatura.
Temos então que no material a, o aumenta com o aumento da temperatura e no material b o diminui com o aumento da temperatura.
Show de bola! Conseguimos responder nossa questão!
Resposta
No material a, o aumenta com o aumento da temperatura e no material b o diminui com o aumento da temperatura.