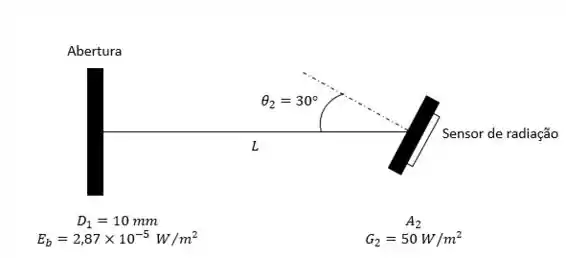
Considere uma abertura de de diâmetro onde a radiação é emitida como um corpo negro com poder emissivo de . O sensor de radiação é posicionado com de inclinação fora do sentido normal da visão, como mostrado na Fig. P12-42. Considerando que o sensor estiver sentindo a irradiação de , determine a distância entre a abertura e o sensor.

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

• A abertura emite difusa como um corpo negro.
• Ambos abertura e sensor podem ser aproximados como superfícies diferenciais desde que ambos sejam muito pequenos se comparados ao quadrado da distância entre eles.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Aproximando ambos abertura () e sensor () como superfícies diferenciais, o ângulo sólido subentendido por quando visto por pode ser determinado por:

A radiação emitida por que atinge é equivalente à radiação emitida por através de um ângulo sólido . A intensidade da radiação emitida por é dada por:

Portanto, a taxa de energia de radiação emitida por na direção de através do ângulo sólido é determinado multiplicando pela área de normal a e o ângulo sólido , isso é:

Sabe-se que , e a irradiação é a taxa na qual a radiação é incidente na superfície por unidade de superfície, então a irradiação medida pelo detector de radiação é: