Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 156

Um modelo de aerofólio com corda de 150 mm e envergadura de 750 mm é colocado em um túnel de vento com um escoamento de ar igual a 300 m/s (o ar está a 20°C). O modelo é montado sob uma haste suporte cilíndrica com 25 mm de diâmetro e 250 mm de altura. Instrumentos na base da haste indicam uma força vertical de 44,5 N e uma força horizontal de 6,7 N. Calcule os coeficientes de sustentação e de arrasto do aerofólio.

Passo 1

Nesse problema, temos alguns dados sobre aerofólio e suporte em túneis de vento, além de medições de elevação e arrasto. Temos que encontrar os coeficientes de sustentação e de arrasto do aerofólio.

Falando um pouco sobre o arrasto, é uma força age sobre um corpo atuando paralelamente à direção do movimento relativo. Para a resolução de questões relacionadas ao assunto, temos as seguintes equações:

C D = F D 1 2 ρ A V 2                         C L = F L 1 2 ρ A V 2    

Passo 2

O problema tem o seguinte diagrama de corpo livre:

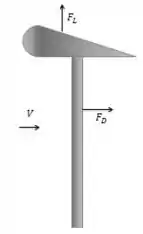
É preciso determinar como os elementos presentes atuam para força total de arrasto, de tal forma que se relacionam assim:

F D = F D c i l i n d r o + F D a e r o f ó l i o  

Agora vamos começar calculando o número de Reynolds, sabendo que ρ = 1,21 k g m 3 e υ = 1,50 × 10 - 5   m 2 / s , logo

R e = V D υ = 300 m s × 25 × 10 - 3 m 1,50 × 10 - 5 m 2 s = 5 × 10 5

Onde o coeficiente de arrasto do cilindro é 1 .

Portanto, a força de arrasto no suporte é:

F D c i l i n d r o = 1 2 C D c i l i n d r o ρ V 2 L c i l i n d r o D c i l i n d r o

  F D c i l i n d r o = 1 2 × 1 × 1,21 k g m 3 × 300 m s 2 × 150 × 10 - 3 × 25 × 10 - 3 m

  F D c i l i n d r o = 204,1   N

Portanto, o arrasto do aerofólio é:

F D a e r o f ó l i o   = F D - F D c i l i n d r o

F D a e r o f ó l i o   = 6,7   N - 204,1   N = - 197,4   N

A área de referência para o aerofólio é: A = L × W = 150 × 10 - 3 × 750 × 10 - 3 = 0,1125   m 2 .

Então, os coeficientes de elevação e arrasto são:

C D = F D 1 2 ρ A V 2 = 6,7 N 1 2 × 1,21 k g m 3 × 0,1125   m 2 × ( 300 m s ) 2 = 0,00109

C L = F L 1 2 ρ A V 2 = 197,4   N 1 2 × 1,21 k g m 3 × 0,1125   m 2 × ( 300 m s ) 2 = 0,032

Prontinho!!

Resposta

C L = 0,032

C D = 0,00109

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um granizo de 0,8 cm de diâmetro caindo livremente no ar a 1 atm e 5 °C. Determine a velocidade terminal do granizo. Considere a densidade do granizo como 910 kg/m³.
Partículas de pó com diâmetro de 0,05 mm e densidade de 1,8 g/cm³ são levantadas pelo ar durante ventos fortes e sobem até uma altitude de 350 m quando o vento se acalma. Estime quanto tempo levará pa
Observa-se que uma partícula de pó com 0,1 mm de diâmetro cuja densidade é 2,1 g/cm³ está suspensa no ar a 1 atm e 25 °C em um ponto fixo. Estime a velocidade ascendente do ar nesse local. Suponha que
Um tronco de pinho cilíndrico de 2 m de comprimento e 0,2 m de diâmetro (densidade = 513 kg/m³) é suspenso por um guindaste na posição horizontal. O tronco está sujeito a ventos normais de 40 km/h a 5
O ar está escoando por um aerofólio simétrico com um ângulo de ataque zero. (a) A sustentação e (b) o arrasto, que agem sobre um aerofólio, serão iguais a zero ou não?