Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 57
Um tronco de pinho cilíndrico de 2 m de comprimento e 0,2 m de diâmetro (densidade = 513 kg/m³) é suspenso por um guindaste na posição horizontal. O tronco está sujeito a ventos normais de 40 km/h a 5 °C e 88 kPa. Desconsiderando o peso do cabo e seu arrasto, determine o ângulo que o cabo fará com a horizontal e a tensão no cabo.
Passo 1
Antes de começar esse exercício, nós vamos lá na tabela A.9 do apêndice A para pegar a viscosidade dinâmica do ar a 5 °C, já que ela independe da pressão, para que depois possamos calcular as demais propriedades. Então teremos:
Então, da equação de gás ideal, podemos calcular a densidade do ar nessas condições, então teremos:
Agora, a viscosidade cinemática pode ser encontrada através de:
Agora, com essas informações, podemos calcular o número de Reynolds para o escoamento, que é dado por:
Então, substituindo os valores conhecidos (lembrando de utilizar a velocidade em m/s), chegamos em:
Passo 2
Então, agora precisamos ir lá na figura 11-34 que vimos nesse capítulo para encontrar o coeficiente de arrasto em função do número de Reynolds que encontramos. Então com o auxílio da figura 11-34 a seguir:
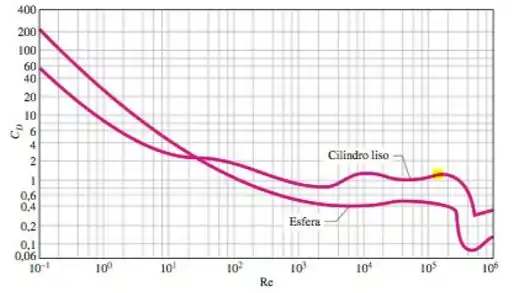
Para o nosso número de Reynolds então, conforme destacado no gráfico acima, teremos:
Então, sabendo que o coeficiente de arrasto é dado por:
E sabendo que a área de escoamento nesse caso é a área transversal frontal do cilindro, dada por:
A equação acima para a força de arrasto se torna:
Substituindo os valores conhecidos, chegamos em:
Agora podemos calcular também o peso do tronco de pinho, que será dado por:
Sendo o volume dado pela área transversal vezes o comprimento do tronco, então teremos:
Substituindo os valores conhecidos, teremos:
Passo 3
Então, a força resultante aplicada no tronco pode ser dada pela soma vetorial do peso e da força de arrasto, então teremos:
Substituindo os valores conhecidos, teremos:
E, então, podemos encontrar a direção do ângulo sabendo que temos um triângulo retângulo, com catetos e , então, o ângulo poderá ser encontrado através de:
Substituindo os valores conhecidos, chegamos em: