Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 90

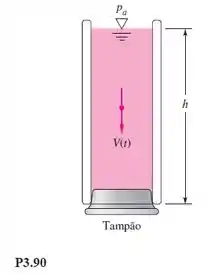
Como mostra a Figura P3.90, uma coluna líquida de altura h é confinada em um tubo vertical de seção transversal A por um tampão. Em t = 0 , o tampão é repentinamente removido, expondo o fundo do líquido à pressão atmosférica. Usando uma análise de volume de controle de massa e da quantidade de movimento vertical, deduza a equação diferencial para o movimento de descida V ( t ) do líquido. Admita escoamento unidimensional, incompressível e sem atrito.

Passo 1

Simbora resolver esse trem!

Cara, ele nos disse que temos as seguintes hipóteses, escoamento unidimensional, incompressível e sem atrito. Vamos trabalhar com isso! O nosso volume de controle é esse tubo, lembrando que o atrito nas paredes é desprezível, assim, fazendo a análise de momento:

∑ F y - b a i x o - ∫ a r e l a t i v a d m = d d t ∫ V b a i x o ρ d υ + m ˙ s a i V s a i - m ˙ e n t r a V e n t r a = 0

Assim, teremos:

m g + Δ p A - τ w A w - a . m = 0

Considerando uma variação de pressão igual a zero, pois teremos pressão atmosfera na entrada e saída, além de lembrar que estamos trabalhando desconsiderando o atrito, teremos:

a = d V d t = g

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estenda o problema P3.46 para o problema de calcular o centro de pressão L da força normal F n , como mostra na figura abaixo. (No centro de pressão, não são necessários momentos para manter a placa e
O braço de um lava-louças rotativo descarrega a 60°C para seis bocais, como mostrado abaixo. A vazão total é de 11,4 L/min. Cada bocal tem um diâmetro de 4,8 mm. Considerando que as vazões dos bocais
A roda d’água da abaixo está sendo acionada a 200 rpm por um jato de água a 45,7 m/s e 20°C. O diâmetro do jato é de 63 mm. Desprezando as perdas, qual será a potência em hp desenvolvida pela roda? Pa
A curva do tubo da figura abaixo tem D 1 = 27 cm e D 2 = 13 cm. Quando água a 20°C escoa através do tubo com 15142 L/min, p 1 = 194k P a (manométrica). Calcule o torque necessário no ponto B para mant
O rotor de uma bomba centrífuga fornece 15142 L/min de água a 20°C com uma rotação de eixo de 1750 rpm. Despreze as perdas. Se r 1 = 150m m , r 2 = 350m m , b 1 = b 2 = 44m m , V t 1 = 3m / s e V t 2