Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 115

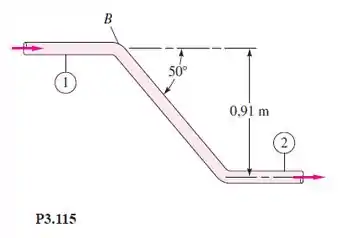
Água a 20°C escoa a 114 L/min através do tubo de 19 mm de diâmetro com duas curvas, como na Figura P3.115. As pressões são p 1 = 206,84   k P a   e   p 2 = 165,47   k P a . Calcule o torque T no ponto B necessário para evitar que o tubo gire.

Passo 1

Simbora lá!

Cara, esse aqui parece o exemplo 3.13 hein, da uma olhadinha lá também!

Vamo lá, primeiro vamo converter essa vazão ai né:

Q = 114 L m i n ⋅ 1   m 3 1000   L ⋅ 1   m i n 60   s = 0,0019   m 3 / s

Belê, temos a massa específica da água na cabeça também, né?! Caso tenha esquecido é ρ = 1000   k g / m 3 , assim, o fluxo mássico é:

m ˙ = ρ Q = 1000 k g m 3 ⋅ 0,0019 m 3 s = 1,9   k g / s

Passo 2

Ok! Vamo descobrir a velocidade no tubo! Considerando um escoamento permanente e que a área não irá se alterar, teremos:

V 1 = V 2 = Q A = Q π 4 D 2 = 0,0019 m 3 s π 4 ( 0,019   m ) 2 = 6,7   m / s

Passo 3

Ta bom, fizemos bastante coisa já! Agora bora considerar que h 1 = 0 e h 2 = 0,91   m , assim, utilizaremos a seguinte expressão (encontrada no exemplo 3.13) para calcular o torque em B:

T B = h 2 p 2 A 2 + m ˙ V 2 - h 1 ( p 1 A 1 + m ˙ V 1 )

Substituindo,

T B = 0,91   m 165470   P a π 4 0,019   m 2 + 1,9 k g s 6,7 m s = 54,3 k g ⋅ m 2 s 2  

Resposta

54,3 k g ⋅ m 2 s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desprezando a resistência do ar, que velocidade atinge um foguete 5s após o seu lançamento vertical a partir do repouso, se a sua massa inicial é de 350k g , a taxa de queima é de 10k g / s e os gases
Considere o veículo mostrado no Problema 4.149. Partindo do repouso, ele é propelido por uma catapulta hidráulica (jato de líquido). O jato atinge a superfície curva e faz uma volta de 180 ° , saindo
O conjunto carrinho/pá de massa m = 30k g , mostrado no Problema 4.128 , é movido por um jato de água. A água deixa o bocal estacionário de área A = 0,02m 2 , com uma velocidade de 20m / s . O coefici
O tanque móvel mostrado pode movimentar ao longo de uma pista horizontal com resistência desprezível. Ele deve ser acelerado do repouso por um jato líquido que se choca contra sua parede curva e é def
Um grande dispositivo de irrigação montado sobre um carrinho descarrega um jato de água com velocidade de 40m / s a um ângulo de 30 ° com a horizontal. O bocal de 50m m de diâmetro está 3m acima do so