Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 14
Mostre que o padrão de escoamento laminar bidimensional
com dp/dx = 0
é uma solução exata para as equações de camada-limite (7.19). Determine o valor da constante C em termos dos parâmetros do escoamento. As condições de contorno são satisfeitas? O que esse escoamento pode representar?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Em primeiro lugar, vamos observar a Equação (7.19b), dada na página 470:
Vamos substituir a função e a velocidade fornecidas no enunciado:
Analisando a equação acima, sabemos que , pois não depende de .
Além disso:
Voltando a substituir isso na equação:
Reorganizando a equação para explicitar :
Demonstramos, assim, que a função satisfaz como solução das equações da camada-limite e ainda encontramos uma expressão para a constante em função da velocidade , que é negativa.
Passo 2
Além disso, podemos demonstrar que as condições de contorno para o escoamento em uma placa plana são satisfeitos para esse perfil de velocidades.
A função tem que garantir . Vamos ver se isso ocorre:
Logo, esta condição é sim satisfeita.
A próxima condição de contorno é . Vamos checar isso:
Pode parecer que irá ao infinito. No entanto, vamos lembrar que no Passo anterior deduzimos que .Logo, e, portanto, , demonstrando que a condição de contorno é satisfeita.
Passo 3
Por fim , o enunciado nos pede pra explicar qual o sentido físico da velocidade ser negativa.
Bem, devemos relembrar que é a velocidade na direção e ela ser negativa, significa que está apontando para baixo, na direção oposta à corrente livre.
Isso significa que temos uma placa plana com drenagem de fluido na parede. Seria algo como a imagem abaixo:
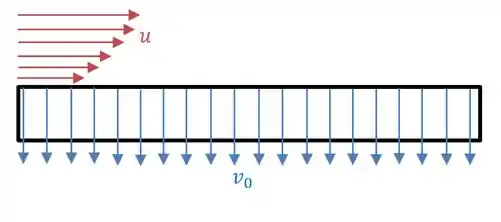
Pronto, matamos a questão juntos!
Resposta
A constante é
A função satisfaz e
O significado físico de é de que temos uma placa plana com drenagem de fluido em sua parede