Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 12
Um objeto bidimensional é submetido a condições isotérmicas nas suas superfícies esquerda e direita, como mostrado no esquema. As duas superfícies diagonais são adiabáticas e a profundidade do objeto é .
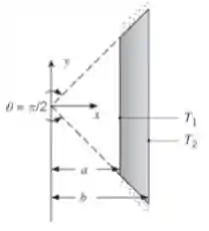
a) Determine o fator de forma bidimensional para o objeto, para e .
b) Determine o fator de forma bidimensional para o objeto, para e .
c) Use a análise alternativa da condução da Seção 3.2 para estimar o fator de forma para os casos a) e b). Compare os valores dos fatores de forma aproximados da análise alternativa da condução com os fatores de forma bidimensionais das partes a) e b).
d) Para e , determine a taxa de transferência de calor por unidade de profundidade para , no caso das partes a) e b).
Passo 1
Letra a)
Para determinar o fator de forma bidimensional para o sistema dado, devemos ir até a Tabela 4.1 “Fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados” e avaliar o Caso 11 (Canal quadrado de comprimento ):
Restrição:
Dados:
;
.
Temos
Então, é dado por:
Como estamos trabalhando com do objeto, temos:
Sendo:
.
Temos:
Passo 2
Letra b)
Seguiremos o mesmo princípio da Letra a):
Restrição:
Dados:
;
.
Temos
Então, é dado por:
Como estamos trabalhando com do objeto, temos:
Substituindo os dados:
Passo 3
Letra c)
Consideraremos uma parede plana elementar de espessura muito pequena, , a uma distância da origem dentro do objeto.
Tomaremos as temperaturas nas faces da parede elementar como e .
Em uma situação de estado estacionário, a taxa de transferência de calor, , através do objeto é constante.
A taxa de transferência de calor através da parede elementar é dada da seguinte maneira:
Aqui, é a área da seção transversal através da qual o calor flui, que é , então:
Separando as variáveis:
Integrando:
Temos que a taxa de transferência de calor em termos do fator de forma é dada como:
Igualando as equações:
Simplificando e isolando :
Passo 4
Para a Letra a)
Dados:
;
;
.
Temos:
Para a Letra b)
Dados:
;
;
.
Temos:
Passo 5
Letra d)
Como dito no Passo 3, a taxa de transferência de calor em termos do fator de forma é dada como:
Dados:
;
;
.
Temos:
Para a Letra a)
Para a Letra b)