Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 118

Um forno tem forma cilíndrica com diâmetro de 1,2   m e comprimento de 1,2   m . A superfície superior tem emissividade de 0,60 e é mantida a 450   K . A superfície da base tem emissividade de 0,50 e é mantida a 800   K . A superfície lateral tem emissividade de 0,40 . O calor é fornecido à partir da superfície da base a uma taxa líquida de 1400   W . Determine a temperatura da superfície lateral e as taxas líquidas de transferência de calor entre as superfícies superior e da base e entre a superfície da base e a da lateral.

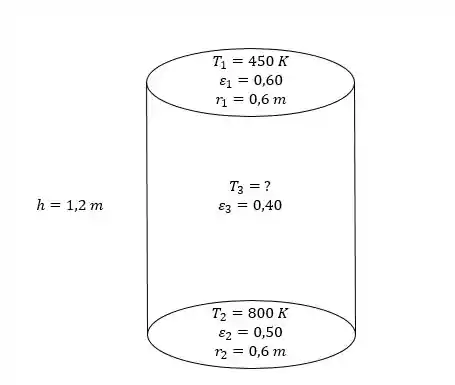
Passo 1

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

  • Existem condições operacionais permanentes.
  • As superfícies são opacas, difusas e cinzas.
  • Transferência de calor por convecção não é considerado.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Passo 2

O fator de visualização da superfície 1 para a superfície 2 é:

L r = 1,2 0,6 = 2 r L = 0,6 1,2 = 0,5 F 12 = 0,17   F i g   13 - 7

As áreas das superfícies são:

A 1 = A 2 = π D 2 / 4 = π ( 1,2   m ) ² / 4 = 1,131   m ²

A 3 = π D L = π 1,2   m 1,2   m = 4,524   m ²

Então os outros fatores de visualização são determinados por:

F 12 = F 21 = 0,17

F 11 + F 12 + F 13 = 1 → 0 + 0,17 + F 13 = 1 → F 13 = 0,83   r e g r a   d a   s o m a ,   F 23 = F 13 = 0,83

A 1 F 13 = A 3 F 31 → 1,131 0,83 = 4,524 F 31 →

F 31 = 0,21   r e g r a   d a   r e c i p r o c i d a d e ,   F 32 = F 31 = 0,21

Agora, aplicaremos a Eq. 13-35 para cada superfície:

Superfície 1:

σ T 1 4 = J 1 + 1 - ε 1 ε 1 F 12 J 1 - J 2 + F 13 J 1 - J 3 ( 5,67 × 10 - 8   W / m 2 . K 4 ) ( 450   K ) 4 = J 1 + 1 - 0,60 0.60 0,17 J 1 - J 2 + 0,83 J 1 - J 3

Superfície 2:

σ T 2 4 = J 2 + 1 - ε 2 ε 2 F 21 J 2 - J 1 + F 23 J 2 - J 3 ( 5,67 × 10 - 8   W / m 2 . K 4 ) ( 800   K ) 4 = J 1 + 1 - 0,50 0,50 0,17 J 2 - J 1 + 0,83 J 2 - J 3

Superfície 3:

σ T 3 4 = J 3 + 1 - ε 3 ε 3 F 31 J 3 - J 1 + F 32 J 3 - J 2 ( 5,67 × 10 - 8   W / m 2 . K 4 ) ( T 1 4 ) = J 1 + 1 - 0,40 0,40 0,21 J 3 - J 1 + 0,21 J 3 - J 2

Passo 3

Agora, aplicaremos a eq. 13-34 para a superfície 2:

Q ˙ 2 = A 2 F 21 J 2 - J 1 + F 23 J 2 - J 3 = ( 1,131   m 2 ) 0,17 J 2 - J 1 + 0,83 J 2 - J 3

E resolvendo as 4 equações que possuímos agora, obtemos como respostas:

T 3 = 831   K

J 1 = 10,477   W / m ²

J 2 = 21,986   W / m ²

J 3 = 22,852   W / m ²

A taxa de transferência de calor entre o fundo e a superfície superior é:

Q ˙ 21 = A 2 F 21 J 2 - J 1 = 1,131   m 2 0,17 21,986 - 10,477 W / m 2 = 2213   W

E a taxa de transferência de calor entre o fundo e a superfície lateral é:

Q ˙ 23 = A 2 F 23 J 2 - J 3 = 1,131   m 2 0,83 21,986 - 22,852 W / m 2 = - 813   W

Resposta

Q ˙ 21 = 2213   W

Q ˙ 23 = - 813   W

T 3 = 831   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere as seguintes fendas, cada uma com largura W, que foram usinadas em um bloco de material sólido.Para cada caso, obtenha uma expressão para o fator de forma da fenda com relação à vizinhança f
Deduza expressões para o fator de forma F12 associado aos arranjos a seguir. Expresse os seus resultados em termos de A1, A2 e qualquer outra área de superfície hipotética apropriada, assim como do fa
Determine F12 e F21 para as seguintes configurações usando o teorema da reciprocidade e outras relações básicas do fator de forma. Não utilize tabelas ou gráficos.Duto longo:Pequena esfera com área A1
Dois objetos convexos estão no interior de um grande recipiente, no qual há vácuo. As paredes do recipiente são mantidas a T 3=300K . Os objetos têm a mesma área, igual a 0,2m 2 , e a mesma emissivida
Considere a cavidade composta por quatro superfícies cinzas e difusas, com todos os lados iguais, mostrada na figura. As temperaturas de três superfícies são especificadas, enquanto a quarta encontra-