Uma parede plana, com espessura de e condutividade térmica de , apresenta uma taxa volumétrica de geração de calor uniforme de e está isolada em um de seus lados, enquanto o outro encontra-se exposto a um fluido a . O coeficiente de transferência de calor por convecção entre a parede e o fluido é de . Determine a temperatura máxima na parede.
Passo 1
Fala Galera!!
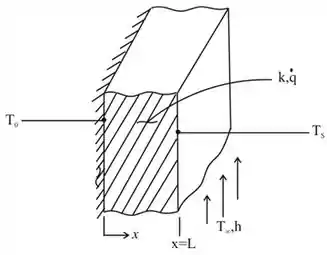
Nessa questão queremos encontra a temperatura máxima na parede, ou seja, queremos a temperatura na superfície isolada da parede. Para isso, podemos fazer o seguinte esquema da parede plana com geração interna de calor, isolada de um lado e exposta a um fluido do outro lado.
Passo 2
PRESSUPOSTOS:
(1) Condições em estado estacionário;
(2) Condução unidimensional com geração de calor volumétrica uniforme;
(3) A superfície interna é adiabática.
DADOS FORNECIDOS:
Espessura da parede:
Condutividade térmica da parede:
Taxa volumétrica de geração de calor uniforme:
Temperatura ambiente:
Coeficiente de transferência de calor por convecção:
Passo 3
Para a condução unidimensional para uma parede plana com geração interna de calor, podemos obter a temperatura máxima na superfície interna isolada da pare pela equação 3.48. Assim temos:
Aqui, é a temperatura da parede na superfície externa, é a temperatura da parede na superfície isolada, é a geração interna de calor, é a espessura da parede e é a condutividade térmica da parede.
Passo 4
Agora, temos que pela equação do balanço de energia na superfície externa da parede, a transferência de calor por convecção deve ser igual a transferência de calor por condução, ou seja:
Assim, podemos encontrar a temperatura na superfície externa da parede pela equação 3.51. Assim temos:
Aqui, é a temperatura ambiente, é o coeficiente de transferência de calor por convecção.
Passo 5
Substituindo a equação do passo 4 na equação do passo 3 temos o seguinte:
Agora, vamos substituir os termos da equação acima pelos dados fornecidos no enunciado. Assim temos:
Portanto, a temperatura máxima na parede é .