Um dissipador de calor de alumínio (), usado para resfriar uma matriz de chips eletrônicos, consiste em um canal quadrado de largura interna , através do qual o fluxo de líquido pode ser assumido para manter uma temperatura de superfície uniforme de . A largura externa e o comprimento do canal são e , respectivamente.

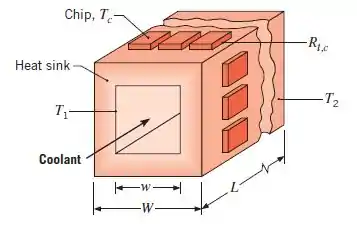
Se fixados às superfícies externas do dissipador de calor mantêm uma temperatura superficial aproximadamente uniforme de e todo o calor dissipado pelos chips é assumido como sendo transferido para o refrigerante, qual é a dissipação de calor por lasca? Se a resistência de contato entre cada chip e o dissipador de calor for , qual é a temperatura do chip?

A taxa de calor total é determinada pela resistência de condução bidimensional da parede do canal,

A resistência pode ser determinada usando a Equação 4.21 com o Caso 11 da Tabela 4.1. Temos que:

Então a equação assume a seguinte forma:

Substituindo os termos da expressão pelos dados fornecidos, temos:

A taxa de calor por chip é então dada pela seguinte expressão:

Substituindo os termos da expressão pelos dados fornecidos, temos:

Portanto, a dissipação de calor por chip é .

Queremos agora encontrar a temperatura do chip, para isso, podemos usar a seguinte expressão:

Reescrevendo a expressão acima isolando a temperatura do chip, temos:

Substituindo os termos da expressão pelos dados fornecidos, temos:

Portanto, a temperatura do chip é .